Анализ прохождения детерминированного сигнала через линейную цепь с постоянными параметрами (курсовая работа), страница 3

2.1.  Смещение копии при  τ Î (0;Т) имеет вид:

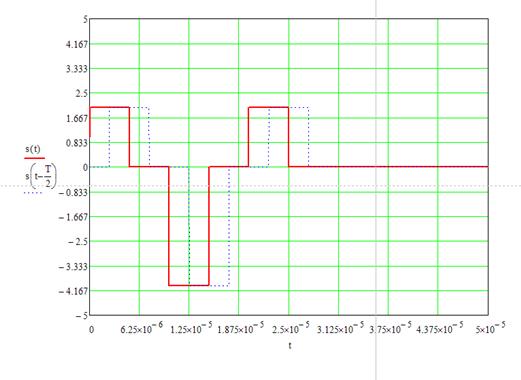
Рисунок 4. Входной сигнал и его смещенная копия при  τ Î (0;Т).

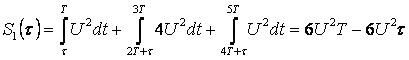
2.2. Смещение копии при  τ Î (Т;2Т) имеет вид:

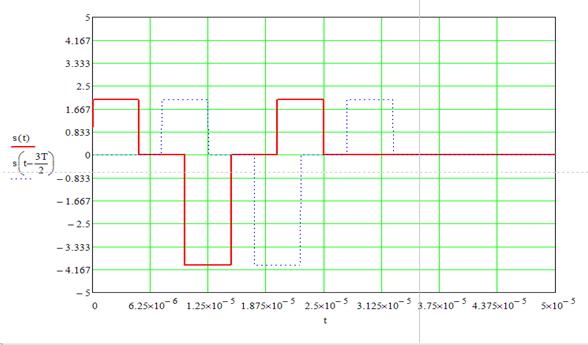
Рисунок 5. Входной сигнал и его смещенная копия при  τ Î (Т;2Т).

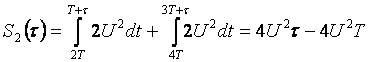
2.3. Смещение копии при  τ Î (2Т;3Т) имеет вид:

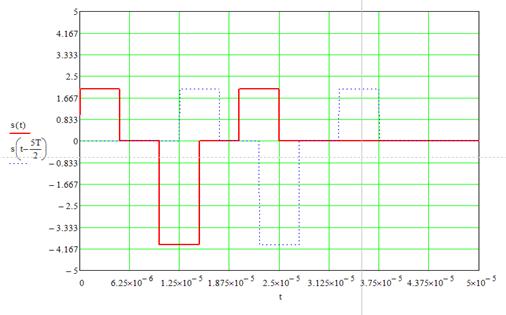
Рисунок 6. Входной сигнал и его смещенная копия при  τ Î (2Т;3Т).

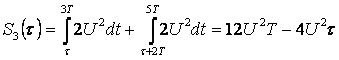
2.4. Смещение копии при  τ Î (3Т;4Т) имеет вид:

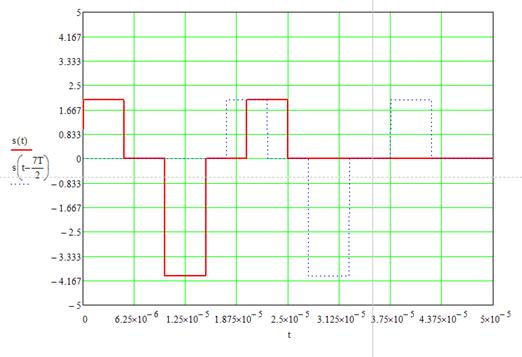
Рисунок 7. Входной сигнал и его смещенная копия при  τ Î (3Т;4Т).

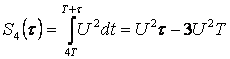
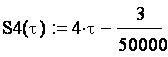
2.5. Смещение копии при  τ Î (4Т;5Т) имеет вид:

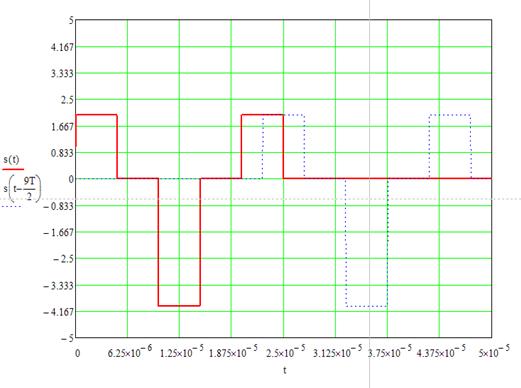
Рисунок 8. Входной сигнал и его смещенная копия при  τ Î (4Т;5Т).

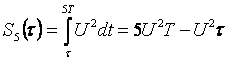
Корреляционная функция на интервале (0;5Т) равна:

                  

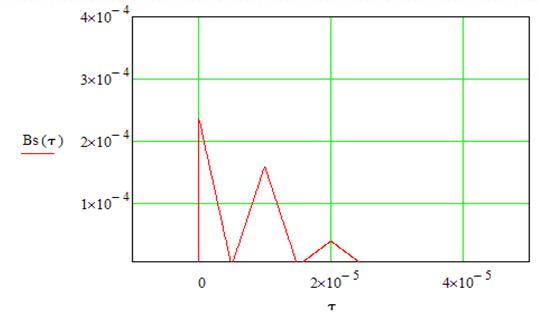
С учетом свойств четности Вs(τ) = Вs(-τ) корреляционная функция имеет вид:

3. Спектр входного сигнала.

3.1. Спектральная плотность входного сигнала.

Спектральная плотность– комплекснозначная функция частоты, одновременно несущая информацию как об амплитуде, так и о фазе сигнала. Модуль выражения спектральной плотности характеризует амплитудный спектр, а аргумент– фазовый спектр.

Опишем сигнал  математически в виде суммы элементарных функций:

Воспользуясь теоремой запаздывания имеем:

Заменяем оператор р на jω и получаем:

3.2. Амплитудный спектр входного сигнала.

Ранее говорилось, что амплитудный спектр – это модуль выражения спектральной плотности. Тогда получим формулу:

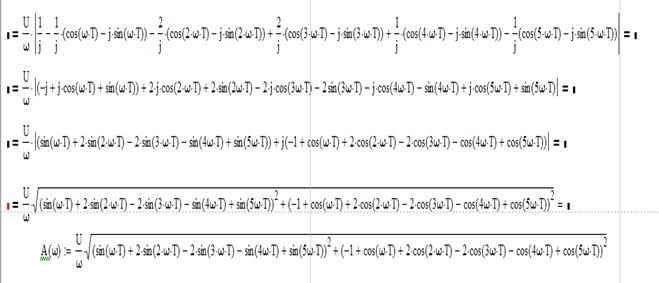
График приведен на рисунке 9: