где ![]() ,
, ![]() ,
, ![]() ,
,
![]() ;
;
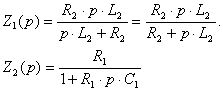
Запишем выражения для ![]() и
и
![]() :
:
![]() =
=![]() ,
,
![]() =
=![]() ,
,
тогда
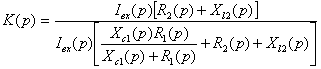
Подставляя ![]() и
и ![]() ,
получим:
,
получим:
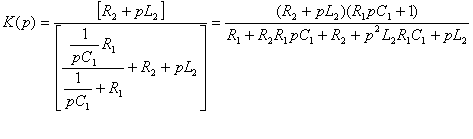
Введем следующие обозначения:
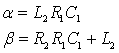
Подставив исходные данные, получим:
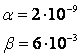
C учетом введенных обозначений K (p) имеет вид:
K (p)=![]()
Заменив p на jω,получим частотный коэффициент передачи в комплексной форме:
![]()
4.2. Амплитудно-частотная и фазочастотная характеристики цепи. Модуль коэффициента передачи определяет амплитудно-частотную характеристику (АЧХ) цепи, то есть можно записать:
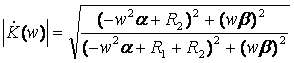
Подставив числовые значения, получим:
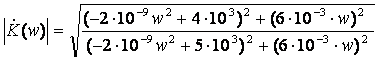
График АЧХ:
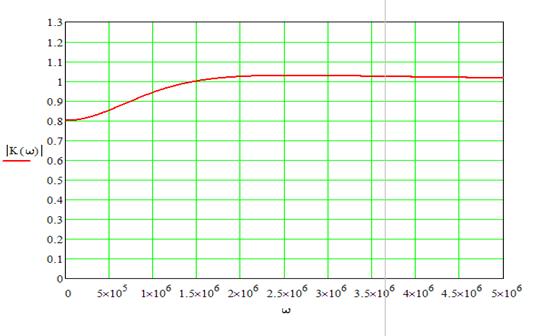
Рисунок 13. Амплитудно-частотная характеристика.
Аргумент коэффициента передачи - фазочастотная характеристика цепи:
![]() ,
,
где
![]() - фаза числителя,
- фаза числителя, ![]() - фаза знаменателя.
- фаза знаменателя.
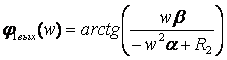
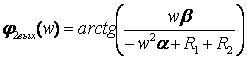
тогда
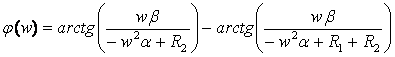
График ФЧХ:
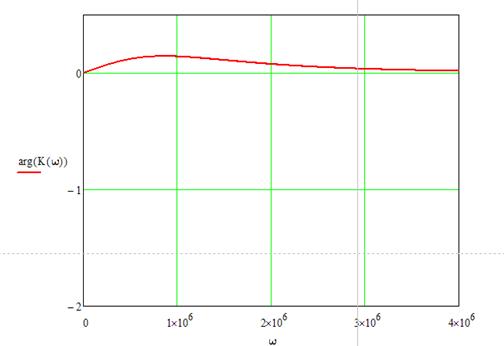
Рисунок 14. Фазочастотная характеристика цепи.
5. Переходная и импульсная характеристики цепи.
5.1. Определение переходной характеристики цепи.
Переходная
характеристика g(t)
- реакция цепи на входной сигнал, описываемый единичной функцией ![]() . Сначала найдем g(t)
в операторной форме, а затем найдем оригинал.
. Сначала найдем g(t)
в операторной форме, а затем найдем оригинал.
Для g(p) верно равенство:
g(p)=K(p)Uвх (p). Так как входной сигнал описывается единичной функцией, то
Uвх(p)=![]() , где
, где
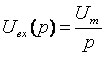 -является изображением ступенчатой
функции.
-является изображением ступенчатой
функции.
Тогда можно записать:
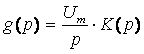
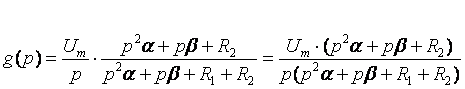
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.