Проблемы процесса ультрафильтрации и пути возможного их решения, страница 9

                                                                                                   (2.17.)

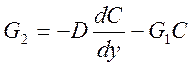                                 (2.18.)

где G1 и G2 – соответственно удельная производительность по растворителю и растворённому веществу;

D – коэффициент диффузии растворённого вещества в растворе.

Введём понятие истинной селективности φи, т. е. селективности с учётом явления концентрационной поляризации:

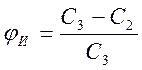, где                                 (2.19.)

С3 – концентрация растворённого вещества у поверхности мембраны.

При допущении постоянства потока растворённого вещества по всей длине пограничного слоя

                               (2.20.)

С учётом  уравнения (2.18.) и (2.19.) получим:

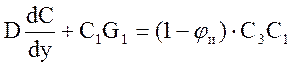                             (2.21.)

Граничными условиями являются:

при y = 0     C = C3

при y =    C = C1

где  - толщина пограничного слоя.

Интегрируя уравнение (2.21.), получим

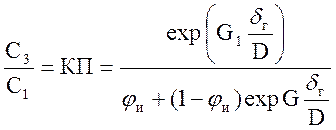                       (2.22.)

Отношение D/ представляет собой не что иное, как коэффициент массоотдачи β растворённого вещества от поверхности мембраны в объём раствора. Введя β в уравнение (2.22.), получим

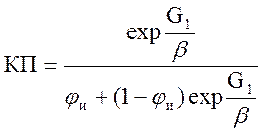                       (2.23.)

В случае φи = 1 предыдущее уравнение упрощается и принимает вид:

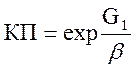                               (2.24.)

2.8. Методы экспериментального определения КП.

Использование для определения величины концентрационной поляризации микроэлектродов. Этот метод основан на применении микроэлектродов для измерения концентрационной поляризации. К недостаткам метода относятся влияние самих микроэлектродов на поток (поляризационный слой), сложность их изготовления и необходимость экранирования металлических частей.

Указанных недостатков лишены оптические методы определения КП. Они позволяют изучать поляризационный слой, не нарушая его структуры. Однако интерферометрический и теневой методы с применением оптических квантовых генераторов в случае сравнительно высокой концентрации разделяемого раствора (>0,2 моль/л) не позволяют исследовать распределение концентраций в слое КП вследствие искривления светового пучка при прохождении через раствор.

Электродиффузионный метод. Сущность его заключается в следующем. При установившемся режиме течения раствора электролита скорость электрохимической реакции определяется скоростью разряда ионов на поверхности электрода, которая может быть выражена дифференциальным уравнением:

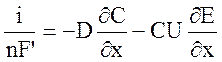, где                                (2.25.)

 i – плотность тока; n – заряд реагирующих ионов;

 F’ – число Фарадея;

 D – коэффициент диффузии ионов в растворе;

 С - -текущая концентрация иона;

 х – координата по нормали к поверхности мембраны;

 Е – потенциал;

 U - подвижность ионов.

Уравнение, применяемое на практике имеет, вид:

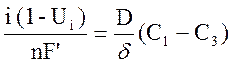, где                              (2.26.)

δ – толщина погранслоя.

Концентрация ионов вблизи электрода зависит то потенциала электрода и при увеличении приложенной разности потенциалов стремится к нулю. При этом плотность тока достигает максимального значения, так называемого предельного iпр

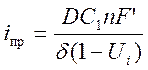                                        (2.27.)

Уравнение можно преобразовать следующим образом:

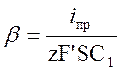                                           (2.28.)

где  z – число принимаемых ионом электронов;

S – поверхность электрода.

Косвенные методы. Один из таких методов основан на использовании истиной селективности мембраны. При этом учитывают зависимость, связывающую концентрацию растворённого вещества у поверхности мембраны с удельной производительностью и коэффициентом массоотдачи:

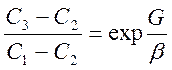                                    (2.29.)

С учётом уравнений (2.25.) и (2.26.) получим

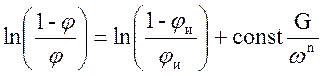                         (2.30.)

Это выражение является уравнением прямой линии в полулогарифмических координатах:

                               (2.31.)

где       y = (1- φ)/φ;          X = G/ωⁿ;              B = (1- φи) / φи