Локальная характеристика массообмена [4] (модифицированный критерий Нуссельта), как уже отмечалось, находиться по экспериментально определённому профилю концентраций:
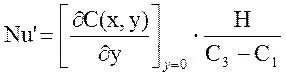 (2.38.)
(2.38.)
Коэффициент массоотдачи, характеризующий интенсивность массопереноса через мембрану, аппроксимируется следующим критериальным уравнением [16]:
![]() (2.39.)
(2.39.)
В критериальном уравнении А – коэффициент, учитывающий, по мнению Козинского, влияние концентрационной поляризации на коэффициент массоотдачи β.Так для УФ альбумина в ячейке с мембраной на вращающемся диске было получено уравнение:
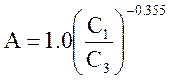 (2.40.)
(2.40.)
В настоящее время вопрос о значении показателя степени n при диффузионном критерии Прандтля не является дискуссионным, и многие авторы считают его равным 0,33, согласно закону затухания турбулентных пульсаций. Величина показателя степени m при критерии Рейнольдса, наоборот, является предметом многочисленных обсуждений, и единства во мнениях по данному вопросу не существует до настоящего времени. Так, некоторые авторы полагают, что для обратного осмоса m изменяется в пределах то 0,3 до 0,4 при ламинарном, и от 0,5 до 0,8 при турбулентном режимах течения потока разделяемого раствора [14].
Достоверность величин приведённых коэффициентов для случаев обратноосмотического разделения растворов в настоящее время считается доказанной. Однако, на основании анализа экспериментальных данных ряд исследователей считают, что применительно к УФ показатель степени m при критерии Рейнольдса в этих уравнениях следует увеличить: в ламинарном режиме – до 0,3÷0,5, а в турбулентном – до 0,75÷1,0. В дальнейшем было выяснено, что при повышении турбулентности системы коэффициент m возрастает, а n при этом снижается.
Экспериментально коэффициенты уравнения (2.39.) определяются следующим образом:
логарифмируя уравнение (2.10.4) и делая обозначение
![]()
получим
![]() (2.41.)
(2.41.)
Построив график зависимости lnNu’ от lnRe’, по отрезку, отсекаемому прямой на оси ординат находим значение B, из которого определяем параметр A. Тангенсом угла наклона прямой к оси абсцисс является ни что иное, как параметр m. Возможность использования этой методики определяется возможностью предварительного определения коэффициента массоотдачи [15].
Обобщая всё сказанное в этом разделе, критериальные зависимости для определения коэффициентов массоотдачи в каналах мембранных аппаратов можно разделить на три группы:
1. Соотношения для определения коэффициентов теплоотдачи, по аналогии, используемые для определения процессов обратного осмоса и ультрафильтрации.
2. Выражения, полученные на основе численных и приближённых решений уравнений переноса массы.
3. Опытные зависимости.
Критериальные уравнения первой группы базируются на аналогии тепло- и массопереноса, поэтому их использование для баромембранных процессов возможно только для приближённого описания [14]. Следует также отметить отсутствие в них зависимости чисел Nu от трансмембранного потока, что существенно отличает их от уравнений второй группы. Последние обычно получают, описывая численные решения уравнений переноса какой-либо аппроксимирующей функцией, которую в дальнейшем преобразуют в критериальную форму. Получение соотношений третьей группы сводится к экспериментальному определению коэффициентов и показателей степеней в критериальных зависимостях. Так как условия проведения экспериментов разными авторами существенно различаются, то результаты опытного определения параметров уравнения третьей группы обычно противоречивы.
Следует
отметить, что критериальные зависимости необходимо применять для расчётов с
особой тщательностью, т. к. авторы приводят их для локальных Nu’ и средних ![]() чисел
Нуссельта. При этом числа
чисел
Нуссельта. При этом числа ![]() и
и ![]() могут быть составлены для полувысоты или
высоты канала.
могут быть составлены для полувысоты или
высоты канала.
Экспериментальное изучение диффузионного сопротивления (КП) в мембранных процессах интенсивно продолжается до настоящего времени.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.