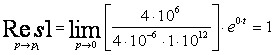
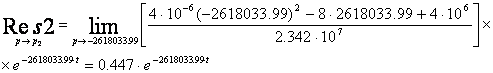
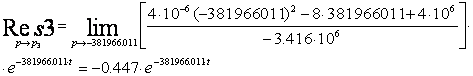
Из теории вычетов известно, что сумма этих вычетов будет
являться оригиналом ![]() :
:
![]()
Окончательное выражение для переходного процесса данной цепи выглядит следующим образом:
![]() (4.5)
(4.5)
С помощью программы Mathcad построим график выражения (4.5):
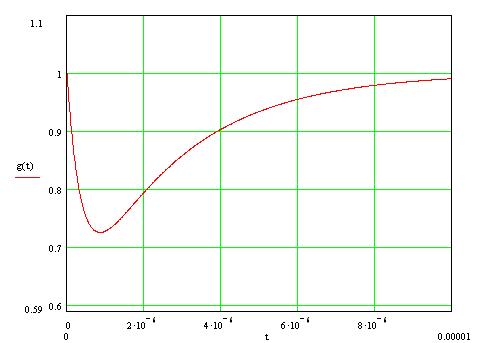
Рис 4.2 График переходного процесса данной цепи
при единичном ступенчатом воздействии.
Для нахождения импульсной характеристики цепи ![]() , необходимо взять производную от
выражения(4.5) переходного процесса по времени, т.е.
, необходимо взять производную от
выражения(4.5) переходного процесса по времени, т.е.
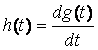 (4.6)
(4.6)
Подставим (4.5) в (4.6) и получим:
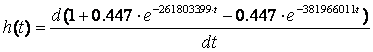
Окончательно имеем:
![]() (4.7)
(4.7)
С помощью программы Mathcad построим график выражения (4.7):
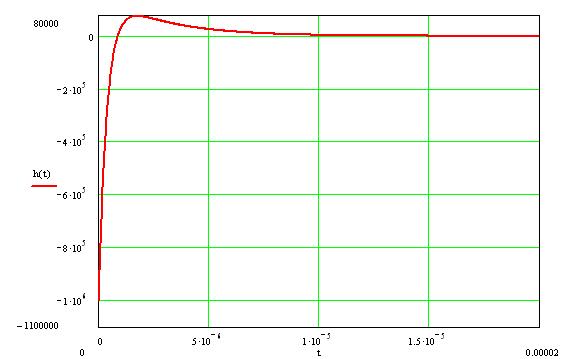
Рис 4.3 График импульсной характеристики данной цепи
при единичном ступенчатом воздействии.
5.Спектр выходного сигнала.
Основная формула спектрального метода, свидетельствующая о том, что частотный коэффициент передачи системы служит множителем пропорциональности между спектральными плотностями сигналов на входе и на выходе выглядит следующим образом:
![]() (5.1)
(5.1)
Анализ систем в частотной области отличается замечательной чертой- эффект преобразовании сигнала в системе отображается просто алгебраической операцией умножения. Справедливо также следующее соотношение:
![]() (5.2)
(5.2)
Подставим выражения (2.2) и (3.1) в (5.2), тогда получим:
с (5.3)
В выражении (5.3) оператор р заменим на комплексное произведение jw:
 (5.4)
(5.4)
Для нахождения амплитудного спектра выходного сигнала необходимо найти модуль комплексного выражения (5.4). Разобьём его на два и преобразуем каждую часть по отдельности.
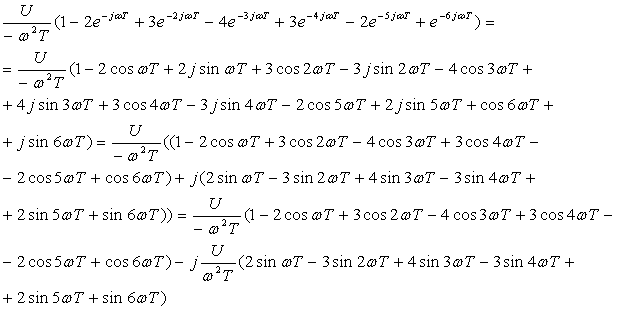
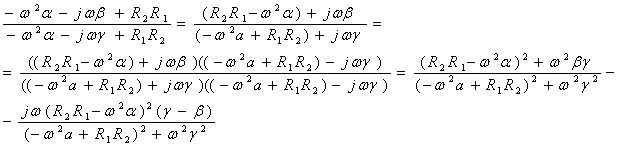
Подставим полученные выражения в равенство (5.4):
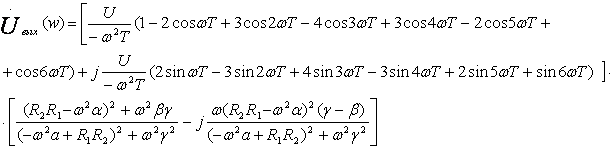
 Окончательно комплексное выражение
для апмлитудного спектра выходного сигнала выглядит так:
Окончательно комплексное выражение
для апмлитудного спектра выходного сигнала выглядит так:
(5.5)
Фазовый спектр выходного сигнала будем искать следующим образом:
![]()
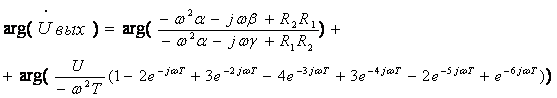
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.