Анализ прохождения детерминированного сигнала через линейную цепь с постоянными параметрами, страница 3

     Корреляционная функция для входного сигнала, сдвинутого на , при  определяется следующей цепочкой интегралов:

     В результате вычислений получим:

1.1.4 Нахождение корреляционной функции для входного сигнала, сдвинутого на  при 

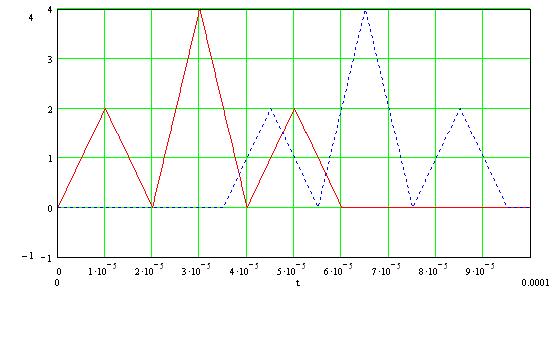
Рисунок 1.1.4 –  Графики входного сигнала  и сдвинутого во времени сигнала  при

     Корреляционная функция для входного сигнала, сдвинутого на , при  определяется следующей цепочкой интегралов:

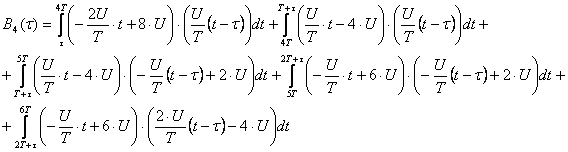
     В результате вычислений получим:

1.1.5 Нахождение корреляционной функции для входного сигнала, сдвинутого на  при 

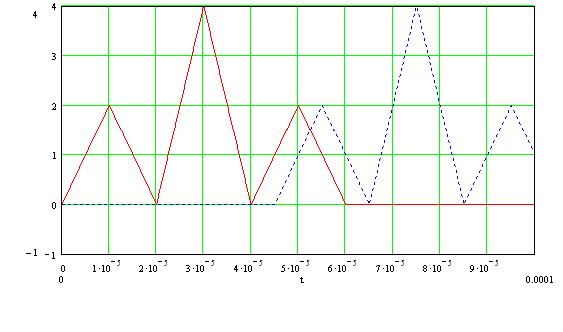
Рисунок 1.1.5 –  Графики входного сигнала  и сдвинутого во времени сигнала  при

     Корреляционная функция для входного сигнала, сдвинутого на , при  определяется следующей цепочкой интегралов:

     В результате вычислений получим:

1.1.6 Нахождение корреляционной функции для входного сигнала, сдвинутого на  при 

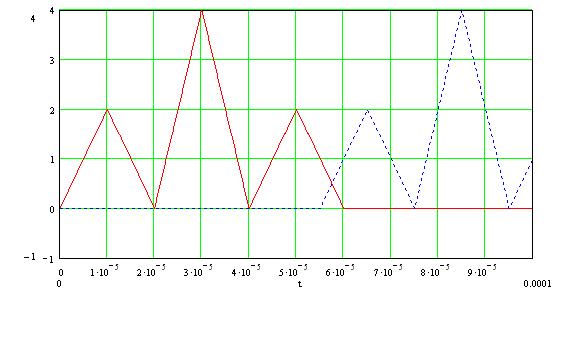
Рисунок 1.1.6 –  Графики входного сигнала  и сдвинутого во времени сигнала  при

     Корреляционная функция для входного сигнала, сдвинутого на , при  определяется следующей цепочкой интегралов:

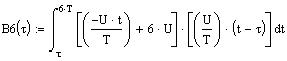
     В результате вычислений получим:

     При помощи функции включения запишем выражение для корреляционной функции на интервале .

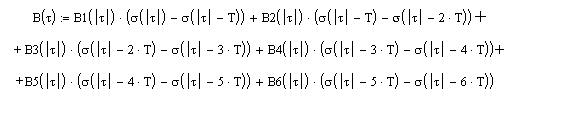
График корреляционной функции представлен на рисунке 1.2.

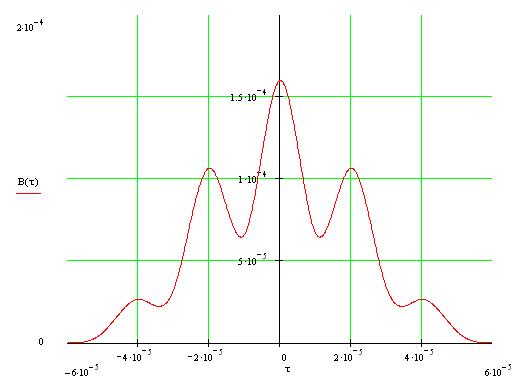
Рисунок 1.2 – Корреляционная функция входного сигнала

                      2.Спектр входного сигнала.

Данный треугольный сигнал можно описать следующей системой уравнений