Анализ прохождения детерминированного сигнала через линейную цепь с постоянными параметрами, страница 6

                                                                                            (3.4) 

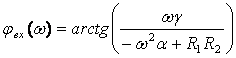                                                                               (3.5)                                                                                                               (3.6)

Теперь, подставив формулы (3.5) и (3.6) в (3.4), получим аналитическое выражение для ФЧХ цепи:

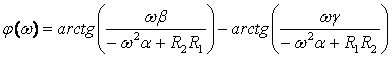  (3.7)

Подставим вместо  и  численные коэффициенты.

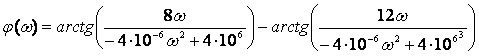                (3.8)

С помощью программы Mathcad построим график выражения (3.8):

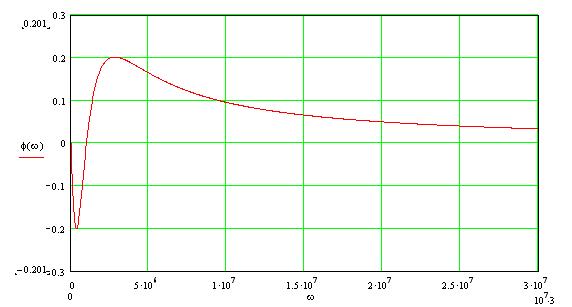
                                        Рис 3.4 График ФЧХ для заданной цепи.

4.Импульсная и переходная характеристики цепи.

Переходной характеристикой цепи является реакция цепи на выходе при воздействии на неё сигнала вида , где -единичная функция. Графически этот сигнал можно представить следующим образом:

                                             

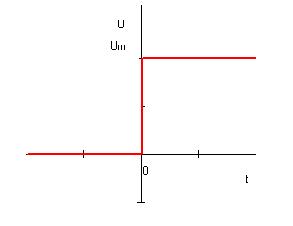
                      Рис 4.1 Изображение ступенчатого входного сигнала.

В теории часто обозначают переходный процесс через . В данном случае будем использовать анализ переходного процесса с помощью преобразований Лапласа. Суть отыскания аналитического выражения для переходного процесса состоит в том, что сначала находят изображение переходной характеристики, далее с помощью обратного преобразования Лапласа, отыскивают оригинал . Для  справедливо следующее соотношение:

                                                                                             (4.1)

где 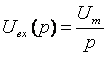-является изображением ступенчатой функции.

Тогда 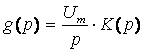                                                                                            (4.2)

Воспользовавшись формулой (3.1) для и приняв , перепишем (4.2) следующим образом:

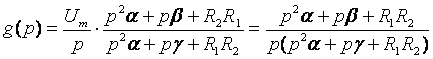                  (4.3)

В выражении  (4.3) необходимо решить квадратное уравнение и привести его к виду:

 .

Найдём корни уравнения и :

      

Найдя корни квадратного уравнения , перепишем выражение (4.3) следующим образом:                                                                                                                              

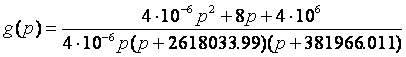                                     (4.4)

Оригинал  будем искать с помощью теории вычетов. Выражение (4.4) имеет 3 полюса, отсюда необходимо найти 3 вычета: