Анализ прохождения детерминированного сигнала через линейную цепь с постоянными параметрами, страница 2

1.Корреляционная функция входного сигнала.                     

При обработке сигналов часто приходится сравнивать сигнал со смещённым во времени копиями этого сигнала, а также другими сигналами. О степени связи сигнала со смещёнными копиями можно судить по корреляционным функциям. Для вещественного сигнала S(t), имеющего конечную энергию на бесконечном интервале времени автокорреляционная функция определяется следующим образом:  

                                   

-интервал сдвига функции.

При таком определении автокорреляционная функция (АКФ) имеет размерность энергии.

В нашем случае мы имеем сигнал треугольной формы, представленный на рис 1.1.

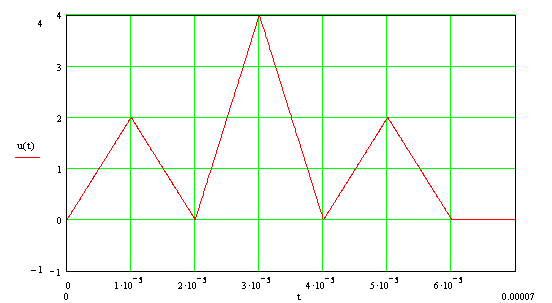
                            рис 1.1 Исходный сигнал треугольной формы.

     На рисунках  (1.1.1), (1.1.2), (1.1.3), (1.1.4), (1.1.5), (1.1.6)  изображен прямоугольный сигнал . Здесь же представлена его “копия”, сдвинутая во времени в сторону запаздывания на с. Произведение  отлично от нуля лишь в пределах интервала времени, когда наблюдается наложение сигналов. Зная, что корреляционная функция четна, рассмотрим ее на интервале . 

1.1.1 Нахождение корреляционной функции для входного сигнала, сдвинутого на  при 

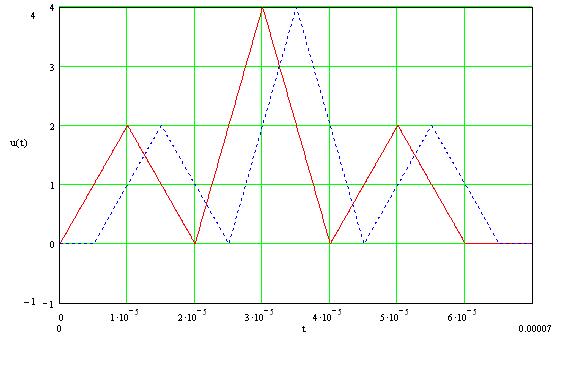
Рисунок 1.1.1 – Графики входного сигнала  и сдвинутого во времени сигнала  при

     Корреляционная функция для входного сигнала, сдвинутого на , при  определяется следующей цепочкой интегралов:

     В результате вычислений получим:

                                  

1.1.2 Нахождение корреляционной функции для входного сигнала, сдвинутого на  при 

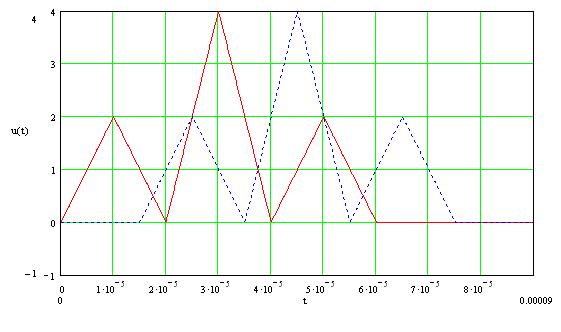
Рисунок 1.1.2 –  Графики входного сигнала  и сдвинутого во времени сигнала  при

     Корреляционная функция для входного сигнала, сдвинутого на , при  определяется следующей цепочкой интегралов:

     В результате вычислений получим:

1.1.3 Нахождение корреляционной функции для входного сигнала, сдвинутого на  при 

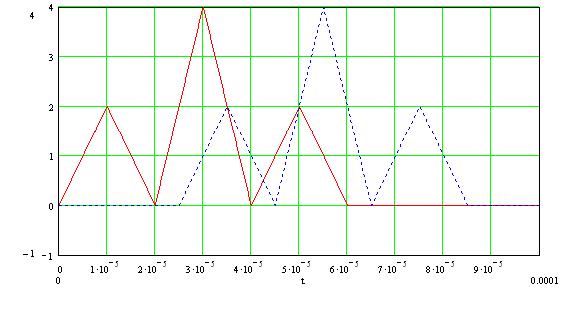
Рисунок 1.1.3 –  Графики входного сигнала  и сдвинутого во времени сигнала  при