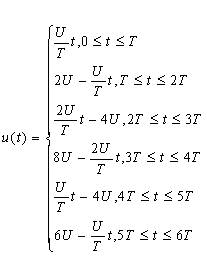
Для построения спектра входного сигнала нам необходимо представить эту систему используя функцию Хевисайда. Тогда сигнал u(t) примет следующий вид:
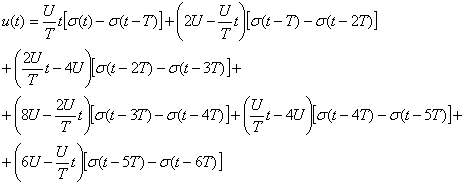 (2.0)
(2.0)
После преобразования получим:
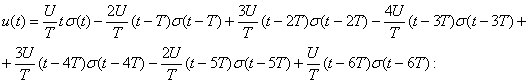 (2.1)
(2.1)
График этого выражения представлен на рис2.1
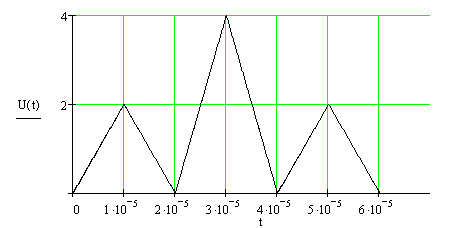
рис2.1 График входного сигнала, заданного с помощью
аналитического выражения (2.1)
Представим аналитическое выражение (2.1) в виде преобразований Лапласа. Функция Лапласа выглядит следующим образом:
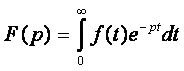
p=jw-оператор Лапласа
Поэтому функция Хевисайда имеет своим изображением следующие выражения:
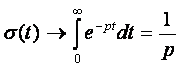
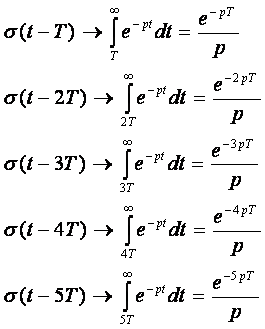
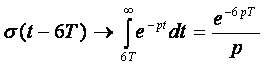
Подставим эти формулы в выражение (2.1):
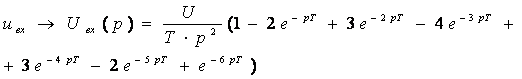 (2.2)
(2.2)
Теперь, согласно правилу перехода к спектральной плотности заменим оператор р на произведение jw (p=jw), тогда получим:
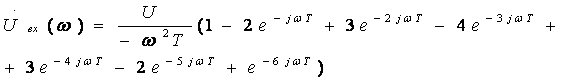
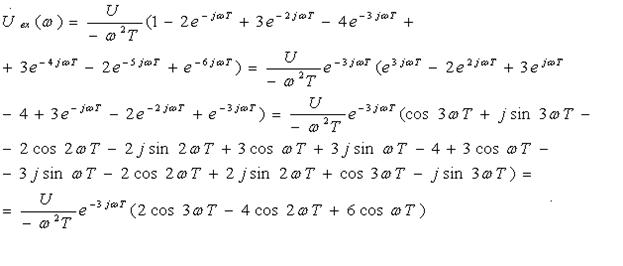
Окончательно получаем
![]() (2.3)
(2.3)
Длятого чтобы найти аналитическое выражение, описывающее спектр входного
сигнала, необходимо найти модуль
полученного выражения (2.3).Все расчёты далее будем производить для
неотрицательных частот(![]() ).
).
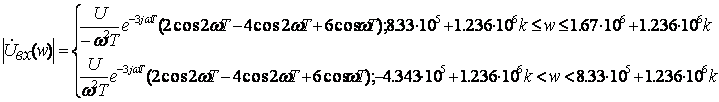 (2.4)
(2.4)
Выражение (2.4) является аналитическим для амплитудного спектра входного
сигнала. С помощью программы Mathcad построим график этого выражения
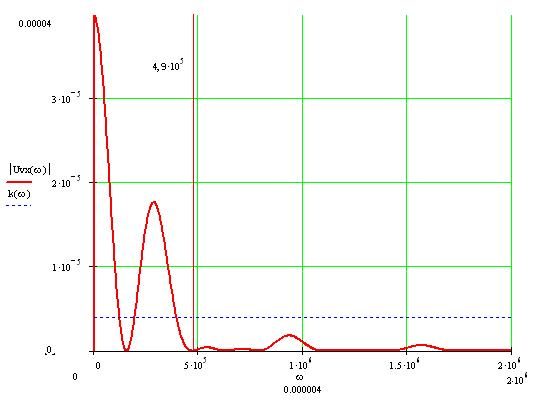
рис2.2 График амплитудного спектра входного сигнала.
Определим графически ширину спектра. Для этого проведём горизонтальный
уровень ![]() .Ширина спектра
приблизительно равна 4.9 рад/с.
.Ширина спектра
приблизительно равна 4.9 рад/с.
Фазовый спектр найдём следующим образом:
![]()
С помощью программы Mathcad построим график этого выражения.
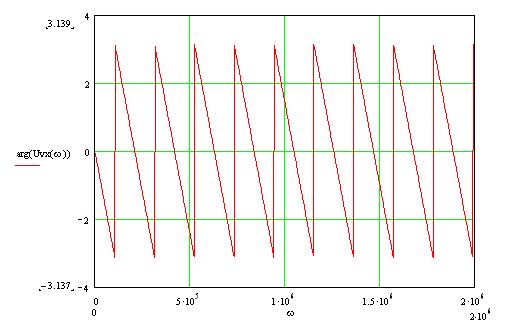
рис2.3 График фазового спектра входного сигнала .
3.Частотный коэффициент передачи цепи.
Анализ начнём с поиска коэффициента передачи цепи в операторной форме К(р).
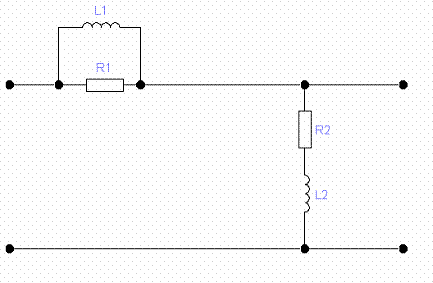 Для этого обратимся к исходной схеме
заданной цепи, представленной на рис 3.1.
Для этого обратимся к исходной схеме
заданной цепи, представленной на рис 3.1.
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.