1. Цель работы: определение средней силы взаимодействия при ударе шаров.
2. Теоретические основы работы.
Несколько упрощенно процесс соударения шаров с одинаковой массой m можно описать так. К моменту соприкосновения паров левый имеет нулевую скорость, а, следовательно, и нулевую кинетическую энергию. Правый имеет максимальную скорость v и максимальную кинетическую энергию.
После соприкосновения левому шару для набора скорости необходимо время t. За это же время правый шар должен передать кинетическую энергию левому шару. Поскольку время t очень мало, возникает большая сила взаимодействия между шарами
F = mv/t
что ведет к деформации шаров и переходу кинетической энергии правого шара в потенциальную энергию деформации шаров
Wn = kx2/2
где k – коэффициент упругости; x - величина деформации.
После, соприкосновения шаров центр масс правого шара продолжает двигаться за счет деформации шаров.
Когда кинетическая энергия правого шара полностью перейдет в потенциальную энергию деформации, начинается обратный процесc - потенциальная энергия деформации переходит в кинетическую энергию левого шара, получающего в результате скорость правого шара.
 Правый шар, получив импульс с обратным знаком, теряет
свою скорость и энергию.
Правый шар, получив импульс с обратным знаком, теряет
свою скорость и энергию.
![]()
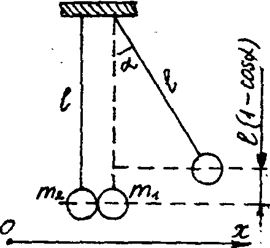
Установка (рис. 1) предназначена для изучения законов сохранения импульса и энергии при ударе двух шаров. Шары массами m1 и m2 подвешены на тонких проволоках длиной l так, что в состоянии равновесия шары касаются друг друга. Если отклонить правый шар на угол a от вертикали и затем отпустить, то в момент прохождения шаром положения равновесия произойдет центральный удар. В результате удара оба шара изменят свои скорости. На установке измеряется время соударения, а также углы отклонения шаров до и после удара.
Применим закон сохранения импульса в момент удара. Закон сохранения импульса имеет место в замкнутой системе взаимодействующих тел - в системе, в которой действуют только внутренние силы, являющиеся результатом взаимодействия тел, входящих в данную систему. Внешние силы, т.е. силы, действующие на тела системы со стороны других тел или полей, в замкнутой системе либо отсутствуют, либо их векторная сумма равна нулю.
|
|
Здесь Рi = mivi -импульс i-го тела, входящего в систему;
n – число взаимодействующих тел в системе.
В реальных условиях невозможно получить идеальную замкнутую систему. Однако и в реальных системах взаимодействующих тел закон сохранения импульса может выполняться при наличии определенных условий. Для системы, состоящей из двух шаров, в момент удара векторная сумма внешних сил - сил тяжести и сил натяжения нитей не равна нулю. Однако проекция внешних сил на ось ОX равна нулю. В этом случае проекция импульса системы на ось будет сохраняться во время удара (сопротивлением воздуха при движении шаров пренебрегаем):
Px = åPxi = const
В дальнейшем изложении индекс x опускаем. Для системы двух соударяющихся шаров запишем закон сохранения импульса в проекции на ось OX:
m1v1,0 + m2v2,0 = m1v1 + m2v2(1)
Здесь v1,0v2,0 – проекции скоростей шаров на ось OX до удара;
v1 и v2 –проекции скоростей шаров после удара. Уравнение (1) можно записать в виде
m1(v1 – v1,0) = -m2(v2 – v2,0)
или
m1Δv1 = - m2Δv2(2)
Разделим (2) на время взаимодействия шаров при ударе t:
m1Δv1/t = -m2Δv2/t(3)
Равенство (3) представляет собой приближенное выражение третьего закона Ньютона F12 = -F21 в проекции на ось OX. Здесь модули векторов F12 и F21 представляют собой средние силы, действующие на каждый из шаров со стороны другого шара. Импульсы сил равны
F12t = m1(v1 – v1,0); F21t = m2(v2 – v2,0) (4)
Пренебрегая силами сопротивления воздуха и, считая удар шаров абсолютно упругим, применим к удару закон сохранения механической энергии:
m1v1,02/2 + m2v2,02/2 = m1v12/2 + m2v22/2 (5)
Решив систему (1) и (5), найдем скорости шаров после удара
V1 = (2m2v2,0 + (m1 – m2)v1,0)/(m1 + m2); v2 = (2m1v1,0 + (m1 – m2)v2,0)/(m1 + m2) (6)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.