1. Цель работы: экспериментальное определение коэффициента внутреннего трения воздуха, определение средней длины пробега молекул воздуха.
2. Теоретические основы работы.
Для определения коэффициента внутреннего трения воздуха в лабораторной работе используется метод, основанный на истечении воздуха через капилляр. Этот метод носит название метода Пуазейля.
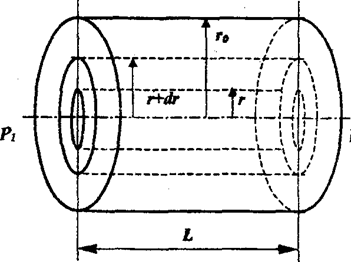 Рассмотрим
ламинарное течение воздуха в капилляре (рис2.1). Течение называют ламинарным,
или слоистым, если поток представляет собой совокупность слоев, перемещающихся
друг относительно друга без перемешивания. Наличие внутреннего трения приводит
к возникновению градиента скорости упорядоченного движения dv/dr. Из
условия симметрии очевидно, что скорость зависит от расстояния r
между рассматриваемой точкой и осью капилляра.
Рассмотрим
ламинарное течение воздуха в капилляре (рис2.1). Течение называют ламинарным,
или слоистым, если поток представляет собой совокупность слоев, перемещающихся
друг относительно друга без перемешивания. Наличие внутреннего трения приводит
к возникновению градиента скорости упорядоченного движения dv/dr. Из
условия симметрии очевидно, что скорость зависит от расстояния r
между рассматриваемой точкой и осью капилляра.
|
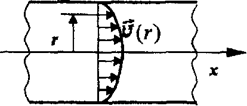
Вырежем мысленно в газе цилиндрический слой (рис 2.2) внутренним радиусом r и внешним радиусом r + dr. На этот слой со стороны более быстрых слоев по закону Ньютона для внутреннего трения действует ускоряющая сила:
F(r) = h*|dv/dr|S, (2.1)
Где S- площадь боковой поверхности цилиндра S=2prL
Со стороны более медленных слоев, прилегающих к выбранному, действует «замедляющая» сила F(r + dr), причём силы F(r) и F(r+dr) направлены в противоположные стороны, результирующая сила, действующая на выбранный слой, может быть найдена с использованием соотношения
F(r + dr) » F(r) + dF,
Тогда F(r) - F(r + dr) = -dF. (2.2)
Опуская знаки модуля и подставив значение S из (2.1) получим:
dF = -2phLd|rdv/dr| (2.3)
Градиент упорядоченной скорости dv/dr<0 самая большая скорость на оси симметрии (рис 2.2), поэтому сила dF - положительная. Эта сила при стационарном течении воздуха равна силе dF', действующей на слой из-за разности давлений p1 – p2
dF’ = (p1 – p2)*dS = (p1 – p2)*2pr*dr (2.4)
Путём математических преобразований из (2.3) и (2.4) получим зависимость упорядоченной скорости U(r):
U = (p1 – p2)*(r02 – r2)/4hL (2.5)
Из выбранного нами слоя (рис 2.2) за время t вытечет объём газа dV = Ut2pdr. Используя соотношение 2.5, получим
dV = p(p1 – p2)t(r02r – r3)dr/2hL (2.6)
|
|
Из последнего соотношения получим формулу Пуазейля:
V = pr04(p1 – p2)t/8hL (2.8)
Из формулы Пуазейля выразим коэффициент внутреннего трения (вязкость) воздуха:
h = pr04t(p1 – p2)/8LV (2.9)
где V-объём воздуха, протекающего через капилляр
t - время истечения данного объёма воздуха
Методами молекулярно-кинетической теории идеального газа получено следующее выражение для коэффициента внутреннего трения:
h = r<l><v>/3 (2.10)
![]() Здесь <v>
= Ö8RT/pm - средняя скорость теплового движения молекул
идеального газа;
Здесь <v>
= Ö8RT/pm - средняя скорость теплового движения молекул
идеального газа;
m - молярная масса; T- температура; R - универсальная газовая постоянная;
<l> - средняя длина свободного пробега молекул, вычисляемая по формуле:
![]() <l> = 1/Ö2*sэфф*n (2.11)
<l> = 1/Ö2*sэфф*n (2.11)
sэфф - эффективное сечение соударения молекул;
n - число молекул газа в единице объёма (концентрация);
r - плотность газа.
З. Описание экспериментальной установки.
|
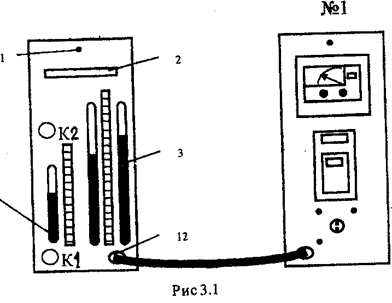 Экспериментальная установка (рис 3.1)
состоит из приборного модуля №1 и функционального модуля №11. На передней
панели функционального модуля расположен крепёжный винт 1, табличка с названием
работы 2, клапан К2 перепуска воды из вспомогательного бачка в мерную ёмкость,
клапан К1 подачи воздуха в мерную ёмкость для перепуска воды из этой ёмкости во
вспомогательную, водяной U-манометр 3 и уровнемер с измерительными шкалами 4.
Экспериментальная установка (рис 3.1)
состоит из приборного модуля №1 и функционального модуля №11. На передней
панели функционального модуля расположен крепёжный винт 1, табличка с названием
работы 2, клапан К2 перепуска воды из вспомогательного бачка в мерную ёмкость,
клапан К1 подачи воздуха в мерную ёмкость для перепуска воды из этой ёмкости во
вспомогательную, водяной U-манометр 3 и уровнемер с измерительными шкалами 4.
|
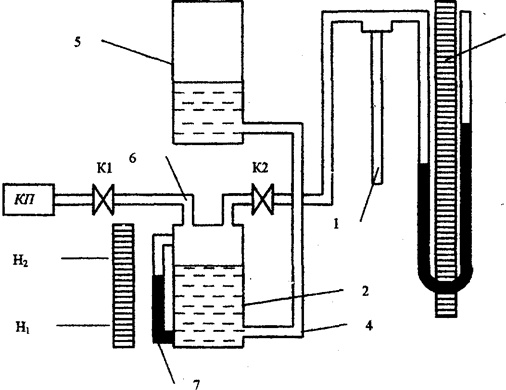
Схема установки (рис 3.2) включает капилляр 1, соединённый одним концом через систему пневмопровода с мерной ёмкостью 2 и U-манометром 3. Другой конец капилляра сообщается с атмосферой. Мерная ёмкость 2 соединена резиновой трубкой 4 со вспомогательным сосудом 5, в котором находится вода. С помощью резиновой трубки б мерная ёмкость соединена с микрокомпрессором приборного модуля. При закрытом клапане К1 и открытом (нажатом) клапане К2 вода из вспомогательной ёмкости 5 через трубку протекает в мерную ёмкость 2. При этом вода вытесняет воздух из мерной ёмкости через капилляр в атмосферу. Объём воздуха, протёкшего через капилляр, определяется по изменению уровня воды в мерной ёмкости. Так как сечение капилляра мало, то возникает разность давления воздуха на его концах, которая измеряется водяным U-манометром.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.