Обобщенные средние функции. О соотношении цены и качества

Лекция

Обобщенные средние функции.

          Будем считать, что полезные качества оцениваемых объектов представляются показателями  . Значению  означает наименьшее проявление - го качества,  а  -  наибольшее. В типичной ситуации, когда определяются рейтинги заданной совокупности однородных объектов по разным качествам,  значения показателей   не требуются.  Если в заданную совокупность добавляется новый объект, то некоторые из   могут выйти из промежутка  ; .  Однако, можно так пересмотреть процедуры вычисления показателей  , что все их значения снова окажутся в . Следует отметить, что теория качеств не накладывает каких-либо ограничений на показатели качеств, допуская любые их значения. 

         Весьма трудной и нечетко определенной ( fuzzy ) задачей является вычисление единого (комплексного) или, иначе говоря, свернутого показателя качества .  Будучи функцией частных показателей  он характеризует объект в целом,  с учетом всех его полезных качеств,  имеющих значение для оценивания.  Традиционный и наиболее распространенный  подход, предписанный в  ГОСТ 24294-80,  но прямо не указанный  в современных стандартах семейства  ISO,  состоит в использовании взвешенных средне-арифметических функций вида:

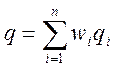                                                                  .                                                           (1)

Числа  называются весовыми коэффициентами или просто весами.  Всегда предполагаемое условие нормированности             

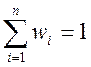                                                                                                                             (2)

эквивалентно тому, что набору  значений   при   отвечает значение

                                                              .

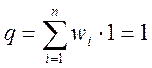Определение 1.  Функция   называется средней, если для любых значений  ее аргументов имеет место:          

                                                                                           (3)

Функция вида (1) является средней в силу условия (2).

Другие примеры средних функций:

средне-геометрическая  функция

,

средне-гармоническая  функция

      

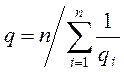
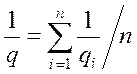
и средне-квадратическая функция

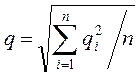
Определение 2. Функция  называется строго монотонной, если для

любых значений  ,   ее аргументов имеет место:          

          ,         <       (4)

         Если все весовые коэффициенты  отличны от нуля,  то функция  (1)  является строго монотонной. Строго монотонным, например, являются средне- геометрическая,  средне-гармоническая и средне-квадратическая функции.  Для строго монотонных функций  условие  (3)  равносильно

                                                .                                            (5)

В самом деле, если , то, выбирая аргументы

 ,

в силу  (4) и (5)  получим противоречие:

.

Аналогично доказывается невозможность .

         Условие (5) имеет очевидный смысл, т.к. значения показателей качества определяют позиции в рейтингах. Если по каждому из частных качеств объект имеет рейтинг  №  m , то в едином  рейтинге ( с учетом всех полезных качеств) он должен занять позицию №  m.  Любой другой выбор разумно объяснить невозможно.

         При переходе от функций вида (1) к произвольным средним  понятие весового коэффициента, вообще говоря, теряет смысл. Хотя квалиметрия  всегда приписывает

частным качествам постоянные веса , включая их даже в нелинейные зависимости , в абстрактной средней функции коэффициентам  места нет.

         В теории качеств было предложено считать весами производные

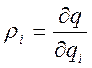                                                                                                                            (6)

от функции единого качества по своим аргументам, которые характеризуют влияние частных качеств  на единое качество . Для функций вида  (1) это определение отвечает обычным весовым коэффициентам, т.е. . Однако, в общем случае свойство (2)  исчезает, и условие нормированности весов

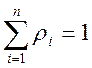                                                                                                                            (7)

отнюдь не обязано выполняться при всех  значениях показателей  . Например, для средне-геометрической, средне-гармонической и средне-квадратической функций  равенство  (7)  имеет место только при равных значениях .

         Следующее определение выделяет класс средних функций, для которых выполнено условие нормированности весов, понимаемых в смысле (6).

Определение 3.   Дифференцируемая функция называется нормализованной средней (НС),  если  и для любых  имеет место

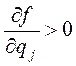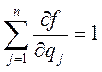                             ,      .                            (8)

        Последнее дифференциальное уравнение означает, что веса  являются нормированными. Отсюда происходит название функции.  Неравенства , очевидно, эквивалентны строгой монотонности функции .  

Замечание.  Всякая нормализованная средняя функция, рассматриваемая  при  ,  где  ,  является средней, строго монотонной функцией .

          Доказательство. Согласно определению 3 достаточно доказать, что имеет место  (3).  Используем формулу конечных приращений Лагранжа