Обобщенные средние функции. О соотношении цены и качества, страница 3

         Переменная  может выражать показатель ценового качества или, иначе говоря, ценовой привлекательности товара.  Его сложно свернуть с показателями технического или потребительского качества,  и используемые для этого методы нельзя признать удовлетворительными. Рассмотрим  два распространенных подхода. 

        Метод 1.  Определяется единый показатель качества товара  без учета цены ,  после чего в качестве единого показателя потребительской привлекательности используется  число -  «полезность на единицу цены». Его также называют интегральным показателем качества, хотя  отнюдь не является средней функцией от  (рис. 3).  Изъян данного метода в том, что пропорциональное изменение цены и качества никак не отражается на показателе . Таким образом, дешевый и плохой товар оказывается одинаково привлекательным по сравнению с дорогим и высококачественным. Это в корне неверно,  хотя при малых отличиях в качествах сравниваемых товаров показатель  применим.   

          Метод 2.  Определяется единый показатель качества  без учета цены,  а также показатель  ценового качества.  Единый показатель качества выражается так:

                                             ,        (),                                      (11)

где  - весовые коэффициенты. Данный метод характерен для квалиметрии.  Его недостаток в постоянстве весов. Очевидно, что для высококачественного товара цена всегда имеет большее влияние на выбор потребителя, чем  качество. Для низкокачественного товара все наоборот:  качество существенно важнее цены. Это означает, что веса   и  качеств  и  зависят от значений этих показателей  (6).

Такое отношение к природе весов составляет главное отличие теории качеств от квалиметрии.  

         Рассмотрим новый подход к вычислению единого показателя потребительской привлекательности товара, связанный с использованием  НС. Следует отметить, что его адекватность и полезность могут быть подтверждены или опровергнуты только в ходе специальных маркетинговых исследований.

         Предположим, что потребительское качество товара выражается показателем ,  вычисление которого составляет отдельную, не обсуждаемую здесь задачу. Если товар является промышленным изделием, то число  выражает его техническое качество и уровень привлекательности для потребителей (brand, имидж и т.п.). Показатель  ценового качества выражает доступность товара для потребителя. Он может быть вычислен с помощью формулы

 ,

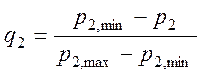где  - цена,  для которой в рассматриваемой совокупности однородных товаров определяются граничные значения  , .  Для оптимизации соотношения цены и качества  в рассматриваемой совокупности товаров следует найти товар, имеющий максимальное значение единого показателя . Будем искать функцию , как некоторую НС, являющуюся многочленом.  Многочлен 1-й степени имеет  вид (11) , в силу чего не представляет интереса. Многочлен 2-й степени имеет график в форме параболоида и, как будет ясно из дальнейшего, для свертывания цены и качества также не годится. Рассмотрим случай НС многочлена  степени 3, описанного в примере 2 . Необходимо определить значения параметров ,,.  Разумно поступить следующим образом.

         Эксперту следует назначить значения  двум маркам товаров, у которых показатели известны. Это нетрудно сделать, рассматривая крайности: дорогой товар высокого качества и дешевый товар низкого качества. В итоге будет получена  система из двух уравнений с неизвестными ,  и останется неопределенным только один параметр.  Рассмотрим конкретный пример на построение рейтинга телефонов марки Sony-Ericsson.