В работе [27] эти модели
применены для синтеза программаторов при следующих ограничениях на управляющее
воздействие: ![]() м3/час, а
м3/час, а ![]() м3/час.
м3/час.
Программатор изменений расхода воздуха для создания газовоздушной атмосферы, блок 6 на рисунке 5.11 имеет закон:
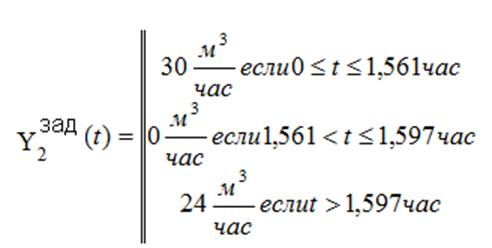
Графическое представление этого закона представлено на рисунке 5.12.
Программатор изменений расхода газа на горение, блок 5 на рисунке 5.11 имеет закон:
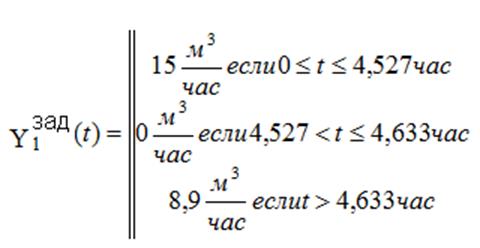 .
.
Графическое представление этого закона представлено на рисунке 5.13.
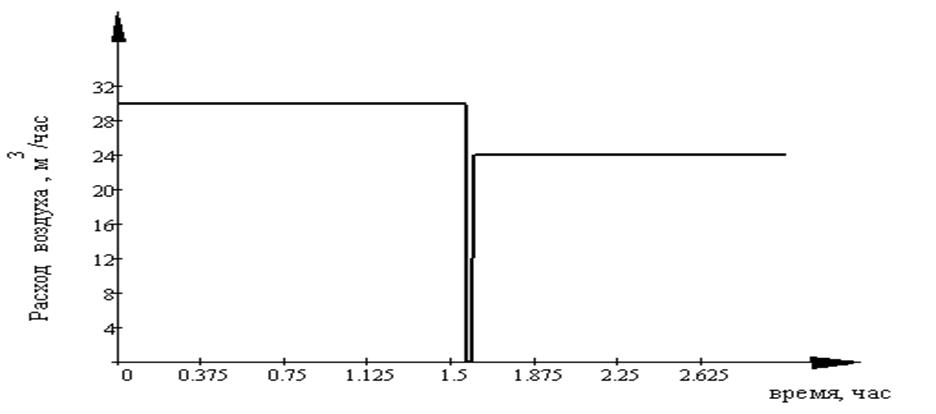
Рисунок 5.12. Эталон изменения задания для расхода воздуха, X2(t)
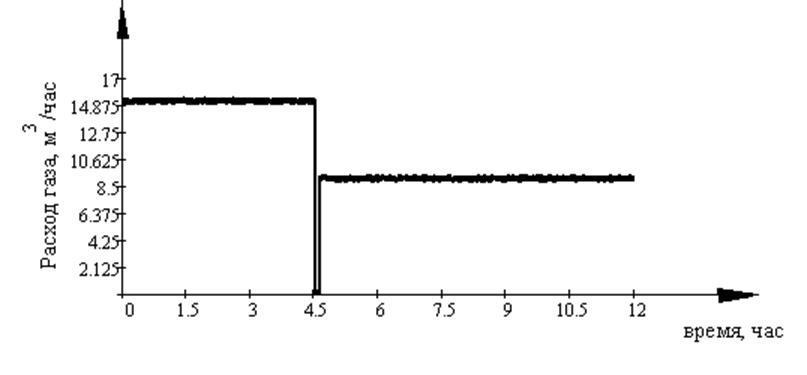
Рисунок 5.13. Эталон изменения задания для расхода газа, X1(t)
Текущие значения эффективности работы эндогазогенератора вычисляются по эталонной математической модели эндогазогенератора (5.12) и имеют вид цифровой последовательности вида:
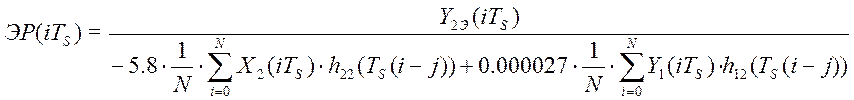 ,
,
где Y2Э(iTS)– текущие значения влажности, измеренные влагомером, X2(iTS) – текущие значения расхода воздуха в газовоздушную смесь, Y1(iTS) – текущие значения температуры в реторте генератора, h22(jTS) – элемент массива импульсной переходной характеристики эндогазогенератора (по каналу управления влажностью эндогаза), h12(jTS) – элемент массива импульсной переходной характеристики по каналу возмущения со стороны температуры реторты, Ts– скважность решётчатых функций (период опроса датчиков, N– длина массивов.
Статическая характеристика
эндогазогенератора (5.10) дрейфует во времени, поэтому основным требованием к
алгоритмам текущей идентификации является его работоспособность и эффективность
в условиях нормальной эксплуатации системы управления. Это возможно только
путем применения статистических методов [66, 68]. Анализ
технологического процесса производства эндогаза показал, что реализации
основных технологических параметров нормального функционирования в
производстве эндогаза представляют собой стационарные случайные процессы.
Поэтому, вся необходимая, для функционирования алгоритма текущей
идентификации, содержится в автокорреляционной функции: 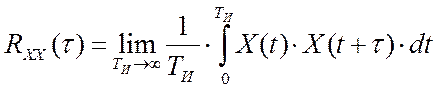 и взаимокорреляционной функции:
и взаимокорреляционной функции: 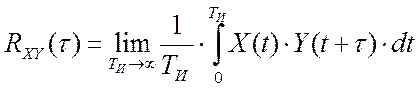 управляющего воздействия, X(t) и критерия управления Y(t). Известно [20], что
существует связь между этими статистическими характеристиками сигналов и
импульсной характеристикой объекта управления:
управляющего воздействия, X(t) и критерия управления Y(t). Известно [20], что
существует связь между этими статистическими характеристиками сигналов и
импульсной характеристикой объекта управления: 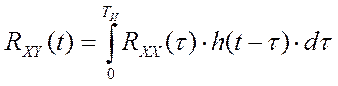 . Поэтому, в работе [27]
разработано программное обеспечение полевого изменяемого прибора [30], которое
позволяет проводить текущую
идентификацию
весовых функций эндогазогенератора по алгоритму (см. гл. 2.2.5):
. Поэтому, в работе [27]
разработано программное обеспечение полевого изменяемого прибора [30], которое
позволяет проводить текущую
идентификацию
весовых функций эндогазогенератора по алгоритму (см. гл. 2.2.5): 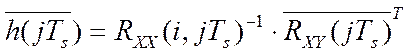 , в котором
, в котором 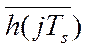 - это вектор строка массива весовых
коэффициентов динамической характеристики идентифицируемого объекта управления.
- это вектор строка массива весовых
коэффициентов динамической характеристики идентифицируемого объекта управления.
![]() - оценка автокорреляционной матрицы управляющего воздействия.
- оценка автокорреляционной матрицы управляющего воздействия.
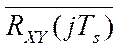 -вектор строка массива взаимокорреляционной функции
управляющего воздействия и критерия управления. Оценка автокорреляционной
матрицы управляющего воздействия,
-вектор строка массива взаимокорреляционной функции
управляющего воздействия и критерия управления. Оценка автокорреляционной
матрицы управляющего воздействия, ![]() .
. 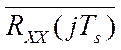 -вектор строка массива
взаимокорреляционной функции управляющего воздействия и критерия управления. После
линеаризации путем разложения в ряд Тейлора в окрестности математического
ожидания множества реализаций управляющего воздействия М{ХJ(iTs)} для автокорреляционной функции и сохранения в
разложении лишь членов первого порядка, имеем [27]:
-вектор строка массива
взаимокорреляционной функции управляющего воздействия и критерия управления. После
линеаризации путем разложения в ряд Тейлора в окрестности математического
ожидания множества реализаций управляющего воздействия М{ХJ(iTs)} для автокорреляционной функции и сохранения в
разложении лишь членов первого порядка, имеем [27]:
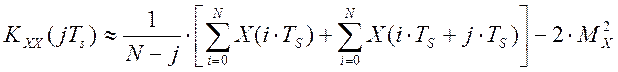 .
.
Линеаризация уравнения для вычисления взаимокорреляционной функции, проведенная путем разложения уравнения измерения в ряд Тейлора в окрестности математических ожиданий множества реализаций стационарного случайного процесса ХJ(iTs) и нестационарного случайного процесса YJ(iTs) , с сохранением в разложении лишь членов первого порядка, дает следующее линеаризованное уравнение для вычисления взаимокорреляционной функции:
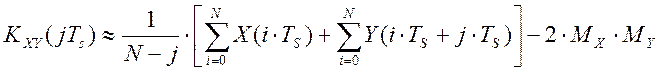
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.