Анализ случайных величин. Планирование многофакторного эксперимента. Адекватность уравнений регрессии и значимость его коэффициентов

Лабораторная работа №1.

АНАЛИЗ СЛУЧАЙНЫХ ВЕЛИЧИН

Цель работы. Найти наивероятнейшее значение  измеряемой  величины (среднее арифметическое  ),  точности  полученных  результатов,   среднюю  квадратическую  и  наибольшую ошибки  среднего  арифметического.

Основные положения.

Результаты  измерений    представляют  собой  случайные  величины.  Процесс  обработки  экспериментальных данных   заключается в нахождении наивероятнейшего значения  измеряемой  величины (среднего  арифметического  ),  точности  полученных  результатов,   средней  квадратической и  наибольшей  возможной  ошибки  среднего  арифметического.

Точность  отдельного  измерения определяется по формуле:

                                     

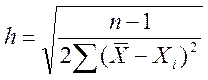
Точности  среднего  арифметического определяется по формуле

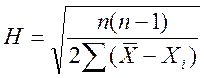
т.е. точность  среднего  арифметического  больше точности  отдельных  измерений  и  пропорциональна  квадратному  корню  из  числа  измерений.  Cредняя  квадратическая  ошибка    среднего  арифметического определяется по  формуле:

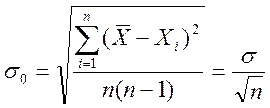
где  -  средняя  квадратическая  ошибка  отдельного  измерения.

          Вероятная  и  наибольшая  возможная  (при  Р-0,997)  ошибки  среднего  арифметического,  соответственно,  равны:

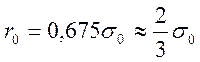  и 

          При  записи  среднего  арифметического  принято  указывать  его  среднюю  квадратическую ошибку.

Порядок выполнения работы

1. Выберите вариант задания( приложение 4)

2.Определите  среднее  арифметическое;

3. Найдите  среднюю  квадратическую  ошибку  отдельного  измерения;

4. Определите  наибольшую  возможную  ошибку    отдельного  измерения  и убедиться,  что  среди результатов  измерений  нет  такий,  которые  отличались  бы  от  среднего  арифметического  более  чем  на  .  Если  бы  таковые  оказались, их  следует  отбросить  и  начать  обработку  сначала. Данные сведите в таблицу;

 5. Определите среднюю  квадратическую  ошибку     среднего  арифметического.

6. Определите характеристики  ,  h  и  H.                        

                 Таблица

Исходные  данные		Первая  обработка		Вторая  обработка
№  по  пор.			()2			()2
1
2
i

Литература

1.  И.И. Кринецкий. Основы научных исследований - Киев - Одесса. Головное издательство объединения «Вища школа», 1981 г.

2.  Л.М. Батунер, М.Е. Позин. Математические методы в химической технике-Ленинград: «Химия»,1968г.

3.  С.А. Ахназарова, В.В. Кафаров. Оптимизация эксперимента в химии и химической технологии  -М.:Высшая школа, 1978 г.

Лабораторная работа №2.

Планирование многофакторного эксперимента

Цель работы. Построение  математической  модели изучаемого объекта с использованием планирования эксперимента.

Основные положения.

 Наиболее эффективным  методом получения  математических моделей  многофакторного процесса является использование метода планирования эксперимента. При  его реализации оценивается роль факторов на которые можно воздействовать ( температура ,концентрации, давления и др. ) при исследовании и оптимизации изучаемого объекта или технологического процесса.

Системы планирования с двумя переменными

Схемы планирования и расчет коэффициентов уравнения регрессии.

Принятые обозначения:

 - средний уровень изменения фактора;

h – шаг варьирования;

                                

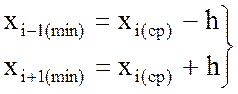
Формулы перевода в условный масштаб для следующие:

                               

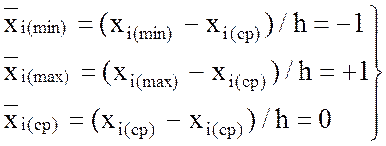
Любое значение х_i, заключенное между переводится в условный масштаб по формуле:

                                  

где  - значение изучаемого фактора  в условном масштабе, а  - в физических. единицах.

Все расчеты с помощью уравнений позволяют осуществлять перевод значения  изучаемого фактора  из натурального масштаба в условный.

Пример расчета.

Если выбранный средний уровень изменения  фактора(x₁)– 1,9 %., а шаг варьирования – 0,6 %, то:

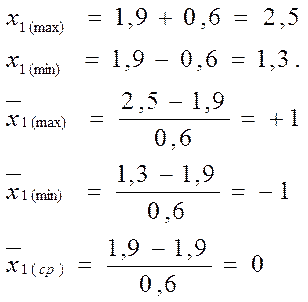
В соответствии с указанным диапазоном свойства  объекта  можно будет изучать в пределах 1,3 % – 2,5 %.

Коэффициенты уравнения для двух переменных рассчитывают по результатам испытания девяти опытов. Количество опытов – девять – определяется числом возможных сочетаний факторов, которые варьируются на трех уровнях .

  Полученное при планировании уравнение регрессии имеет следующий вид:

,                   

где b_0, b_1, b₂, b₁₁, b₂₂, b₁₂- коэффициенты уравнения, х₁, х₂ – количественные величины исследуемых факторов в условном масштабе.

    В качестве R (изучаемое свойство) можно рассматривать любой технический или экономический показатель, характеризующий свойство или себестоимость изучаемого объекта, компонентов или другие оценки изучаемых факторов в условном масштабе. В таблице 1 перечислены значения факторов для расчета коэффициентов уравнения.