

























Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ
/ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ/
«МАИ»
Кафедра динамики и управления летательных аппаратов
ЗАЩИЩЕНО УТВЕРЖДАЮ
с оценкой ______________ Заведующий кафедрой 106
___________ /__________/ ___________ А.В. Ефремов
Проверил:
___________ Ю.В.Тюменцев
Исполнитель:
Студент группы 01-414 _______________О.А.Агафонов
Москва 2009
Содержание:
1. Формулировка задачи.
Для самолета Су-15 на высоте H=4 км и М=0,7 требуется:
1. Разработать линеаризованную математическую модель возмущенного движения при управлении рулем направления.
2. Вычислить матрицы динамических коэффициентов и матрицы управления.
3. Для линеаризованной модели возмущенного движения самолета в канале курса с постоянной скоростью решить задачу АКОР.
4. Решить квадратичное матричное уравнение Риккати.
5. Вычислить коэффициенты усиления оптимального регулятора.
6. Вычислить собственные значения замкнутой системы с оптимальным регулятором.
7. Определить частоты и относительный коэффициент демпфирования разомкнутой и замкнутой системы управления.
8. Сравнить расположение полюсов разомкнутой и замкнутой системы управления.
9. Определить ЛАФЧХ замкнутой системы управления.
10. Определить характеристики переходного процесса для самолета с оптимальным регулятором.
2. Исходные данные.
Самолет: А-10а(США)

Моменты инерции:
![]()
Характеристики атмосферы на заданной высоте:
![]()
![]()
![]()
![]()
Скоростной напор:
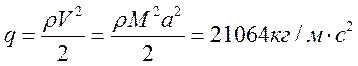
Аэродинамические коэффициенты моментов:
![]()
![]()
![]()
![]()
![]()
3. Формирование математической модели и определение передаточных функций системы управления.
В общем случае в инерциальной системе координат уравнения движения самолета как твердого тела записываются в виде:
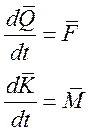
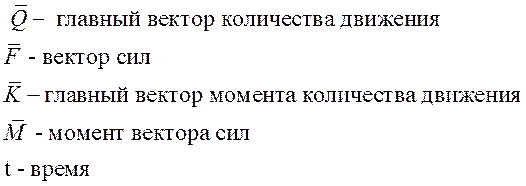
3.1 Уравнения поступательного движения центра масс самолета:
В неинерциальной СК добавляются переносная и кориолисова силы инерции:
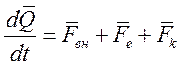
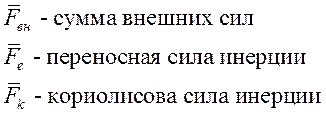
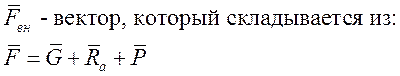
Масса самолета считается постоянной: m=Сonst, тогда:
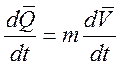
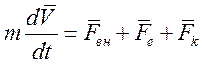 -
запись уравнения движения в неподвижной системе координат.
-
запись уравнения движения в неподвижной системе координат.
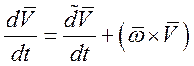 -
связь подвижной и неподвижной СК.
-
связь подвижной и неподвижной СК.
![]() -
локальная производная скорости в подвижной СК.
-
локальная производная скорости в подвижной СК.
За неподвижную
СК принята земная СК ![]() начало которой находится в
центре Земли, а оси жестко закреплены и вращаются вместе с ней.
начало которой находится в
центре Земли, а оси жестко закреплены и вращаются вместе с ней.
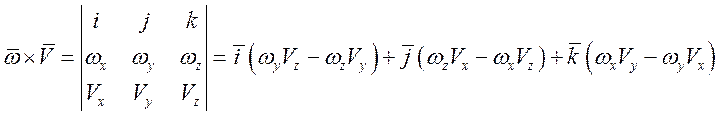
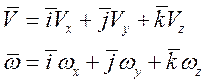
![]() -
проекции вектора вращения подвижной системы координат относительно стартовой на
оси этой системы.
-
проекции вектора вращения подвижной системы координат относительно стартовой на
оси этой системы.
![]() -
проекции вектора линейного перемещения подвижной системы координат относительно
стартовой на оси этой системы.
-
проекции вектора линейного перемещения подвижной системы координат относительно
стартовой на оси этой системы.
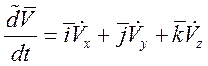
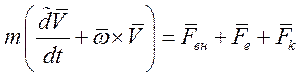
В проекции на оси подвижной СК:
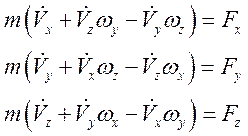
Динамические уравнения сил в траекторной системе координат (при отсутствии ветра):
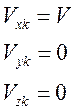
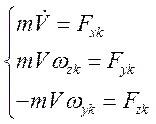
Угловая скорость вращения траекторной СК относительно земной:
![]()
где ![]() -
переносная угловая скорость нормальной СК относительно земной. Появляется
вследствие кривизны Земли. До скорости 1000м/с ее можно не учитывать.
-
переносная угловая скорость нормальной СК относительно земной. Появляется
вследствие кривизны Земли. До скорости 1000м/с ее можно не учитывать.
![]() -
угловая скорость вращения траекторной системы относительно нормальной.
-
угловая скорость вращения траекторной системы относительно нормальной.
![]()
В проекции на траекторную систему координат:
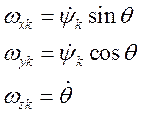
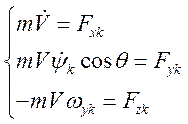
Силы, действующие на самолет и их проекции:
1) Сила тяги:
Задается в связанной системе координат
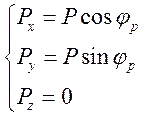
2) Сила тяжести:
Задается в нормальной системе координат
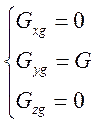
3) Аэродинамическая сила:
Задается в скоростной системе координат
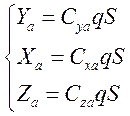
Кориолисова сила инерции практически не проявляется до скоростей порядка 1000м/с, поэтому ее можно не учитывать.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.