Разработка линеаризованной математической модели возмущенного движения при управлении рулем направления самолета Су-15. Вычисление матрицы динамических коэффициентов и матрицы управления, страница 2

Преобразование вектора, заданного в одной системе координат, в другую систему координат происходит через матрицу направляющих косинусов.

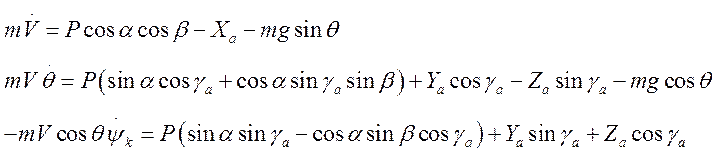
 Запишем данные уравнения в перегрузках:

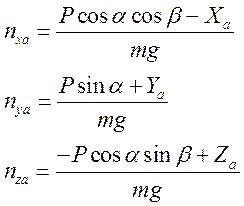
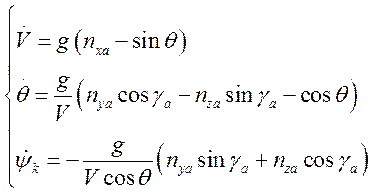
Добавим к этой системе уравнения, связывающие пространственное движение самолета с :

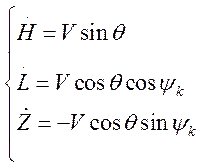
3.2 Уравнения вращательного движения самолета вокруг центра масс:

В земной системе координат:

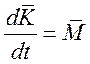, относительно центра масс

По аналогии с поступательным движением:

Локальная производная момента импульса в подвижной СК

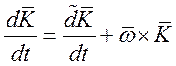
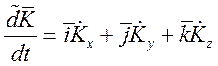
, где - тензор инерции.

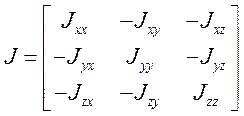
В связанной СК . Так как самолет имеет плоскость симметрии XOY, то ==0.

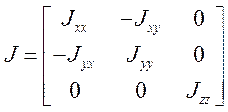
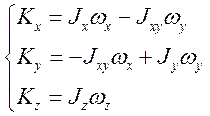
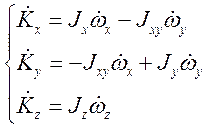
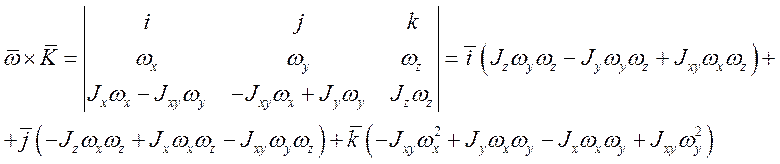
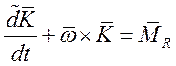
Подставив сюда, получим уравнения движения самолета относительно центра масс:

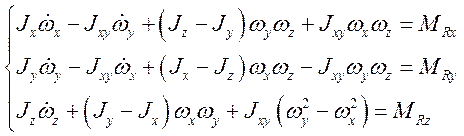
Выражаем угловые скорости:

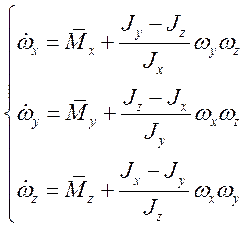
Так как  самолет имеет плоскость симметрии, мы имеем право разбить систему уравнений пространственного движения на две независимых системы: продольного и бокового движений.

Система уравнений для бокового возмущенного движения примет вид:

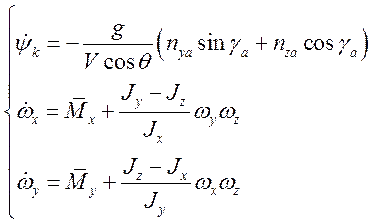
Добавим угловые соотношения из связанной СК:

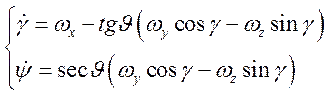
Кинематические соотношения:

Введем фазовую координату :

В итоге для бокового возмущенного движения получаем:

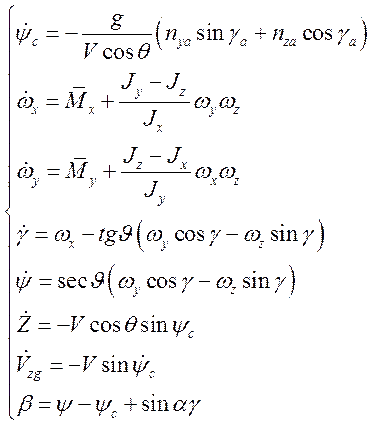
3.3 Линеаризация возмущенного движения:

Линеаризация функции в окрестности значения аргументов – разложение функции в ряд Тейлора по первым членам в этой окрестности.

В качестве опорного режима возьмем горизонтальный установившийся полет без крена и скольжения. Из-за принятых допущений, переходя к приращениям значений знак

можно опустить.

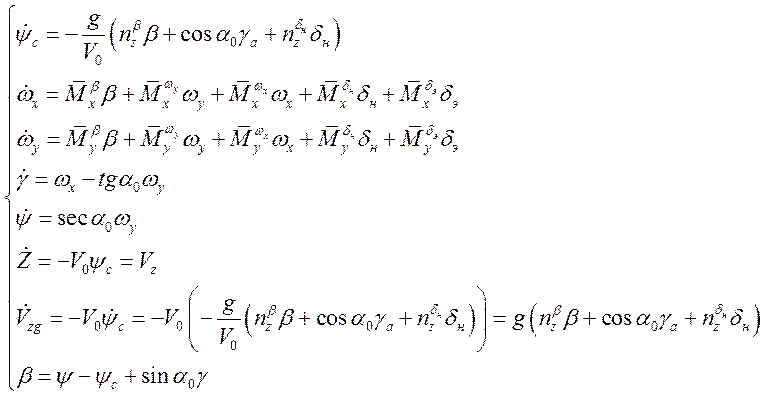
Введем фазовую координату:

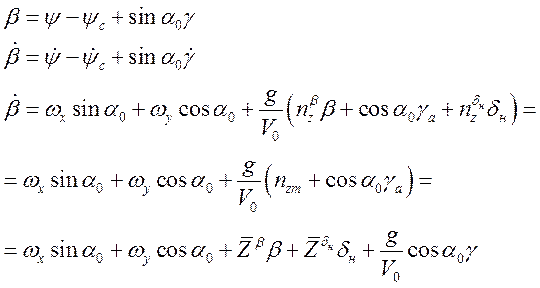
Где:

 ,

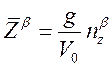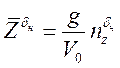
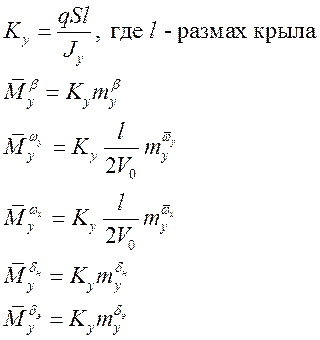
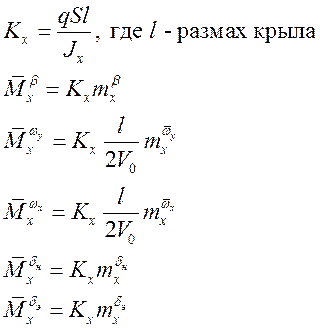
Сгруппируем уравнения так, чтобы слева были фазовые переменные:

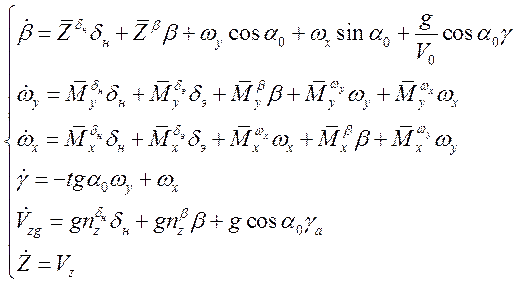
Проведем преобразования Лапласа  и приведем к матричному виду:

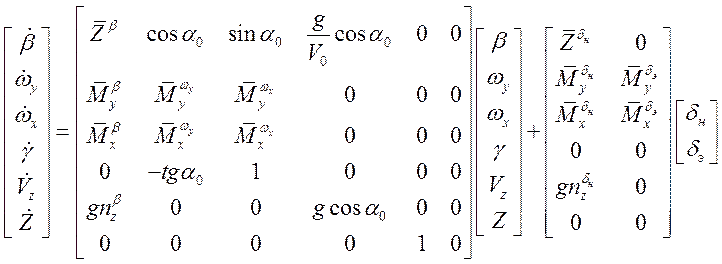
При этом первые четыре уравнения отвечают за угловое (короткопериодическое) боковое движение, а последние два за траекторное (длиннопериодическое) боковое движение.

На малых углах атаки боковое движение можно рассматривать как два изолированных движения: изолированное движение по крену и изолированное движение по рысканию.

Исключим первое уравнение, поскольку угол рысканья фактически в него не входит, а получается простым интегрированием угловой скорости, и матрица получается вырожденной.

Для изолированного движения по рысканью будем рассматривать второе уравнение, приняв =0 и =0.

Получим следующий закон управления:

4. Задача АКОР

4.1 Вычисление матриц динамических коэффициентов и управления.

Система уравнений движения самолета приводится к матричному виду

где  - вектор переменных состояния

 - вектор переменных управления

A, B – матрицы постоянных коэффициентов, характеризующие динамику данной системы:

Подставляя числовые значения:

Получим матрицы:

4.2 Синтез закона управления.

Закон управления системой синтезируется в виде

Где К – постоянная матрица коэффициентов усиления, значения которых выбираются так, чтобы минимизировать оптимизирующий функционал:

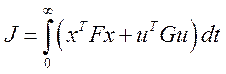
Где весовые матрицы F и Gвыбираются методом Брайсона:

,

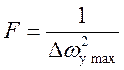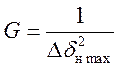
Здесь ,  - желаемые максимальные значения фазовых координат и управлений в процессе регулирования

Для анализа влияния численных значений компонент весовых матриц рассмотрим несколько вариантов:

1-й вариант:

Подставляя числовые значения, получаем матрицу:

,

2-й вариант:

Подставляя числовые значения, получаем матрицу:

,

3-й вариант:

Подставляя числовые значения, получаем матрицу:

,

4.3 Синтез оптимального регулятора.

Для синтеза оптимального регулятора используется пакет программ Matlab7.7.0(R2008b)

1. Воспользуемся процедурой lqr, которая осуществляет проектирование линейно-квадратичного оптимального регулятора для систем непрерывного времени:

[K,S,E]=lqr(Ar,B,F,G)

K – оптимальное статическое матричное звено такое, что использование его в цепи обратной связи в пространстве состояния:

минимизирует функционал:

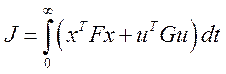
S – решение алгебраических уравнений Рикатти

Е – собственные значения замкнутой системы

2. Введем единичную матрицу:

C = eye(1)

D = 0

С помощью процедуры ss создаем модель пространства состояния по заданным матрицам Ar, B, C, D

raz=ss(Ar,B,C,D)

3. Определим частоты и коэффициенты относительного демпфирования разомкнутой системы.

damp(raz)

4. Составим модель замкнутой системы:

A=Ar-B*K

zam=ss(A,B,C,D)

5. Определим частоты и коэффициенты относительного демпфирования замкнутой системы:

damp(zam)

5. Характеристики систем управления