Разработка линеаризованной математической модели возмущенного движения при управлении рулем направления самолета Су-15. Вычисление матрицы динамических коэффициентов и матрицы управления, страница 3

5. 1 Характеристики системы управления (1-й вариант)

K = -0.8647

S = 19.6300

E = -5.0635

Eigenvalue      Damping     Freq. (rad/s) 

 -3.08e-002     1.00e+000      3.08e-002   

A =-5.0635

 Eigenvalue      Damping     Freq. (rad/s) 

 -5.06e+000     1.00e+000      5.06e+000   

5.1.1 Расположение полюсов самолета с системой управления

1)  Разомкнутая система (без автопилота)

pzmap(raz)

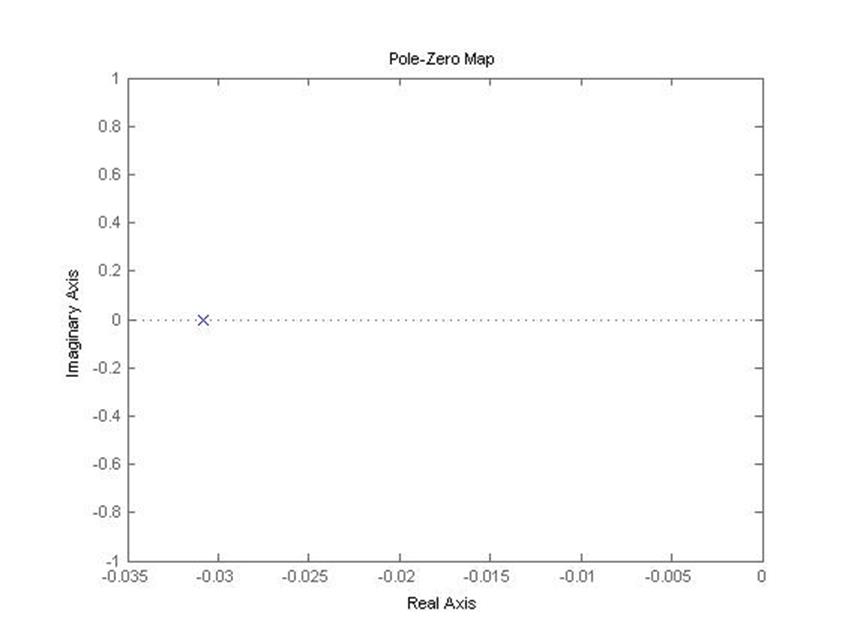
2)  Замкнутая система (с автопилотом)

pzmap(zam)

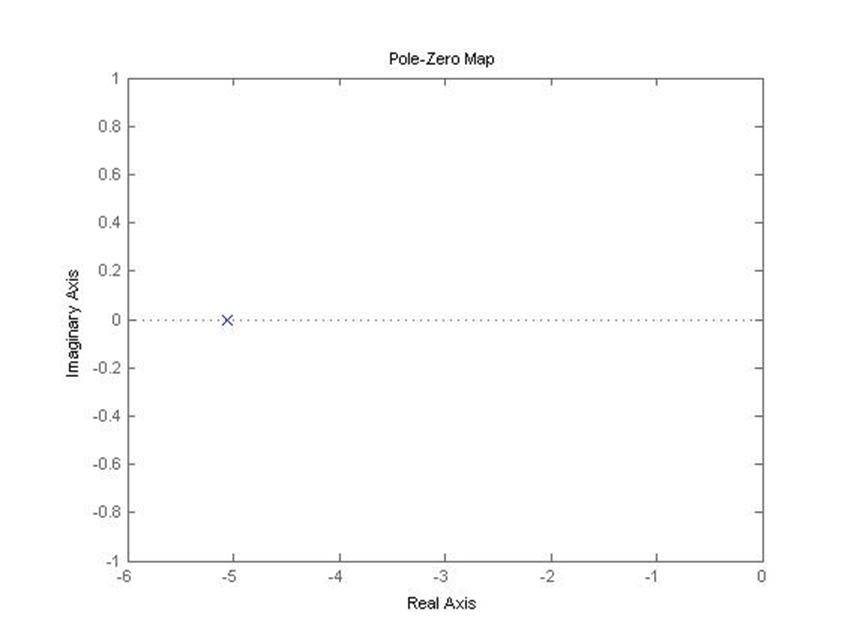
5.1.2 Логарифмические амплитудно-фазовые характеристики разомкнутой системы (самолет с автопилотом)

bode(raz)

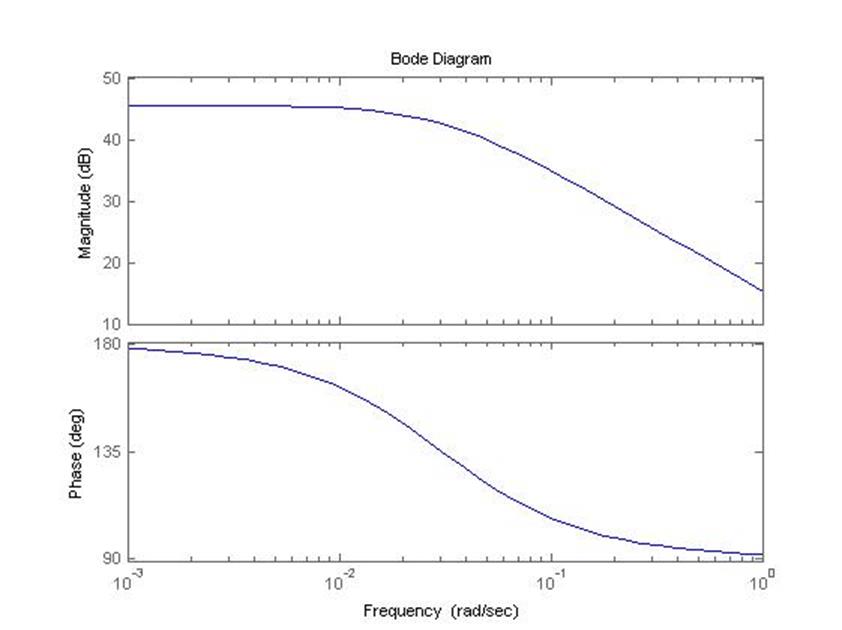
5.1.3 Годограф Найквиста замкнутой системы (самолет с автопилотом)

nyquist(zam)

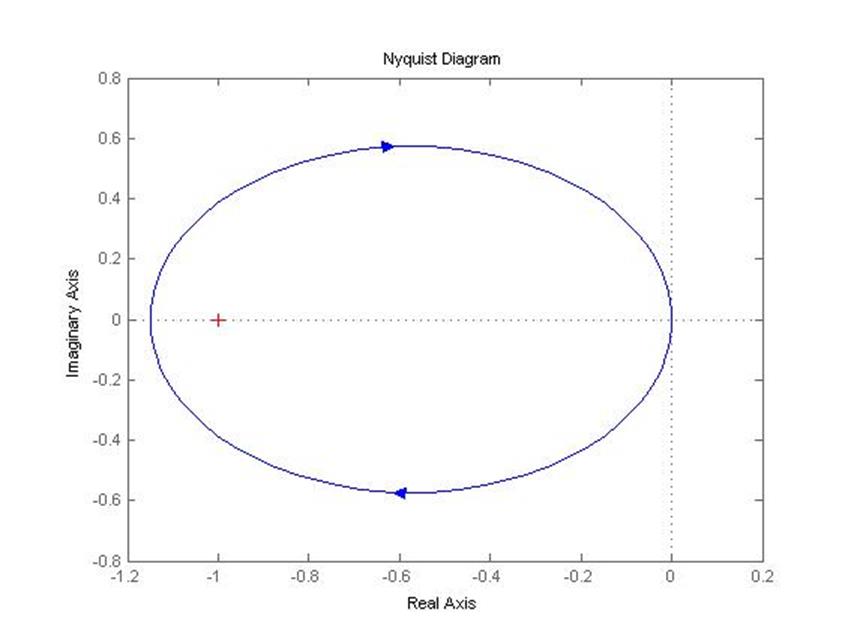
5.1.4 Реакция замкнутой системы на ступенчатое отклонение (отклонение руля направления)

step(zam)

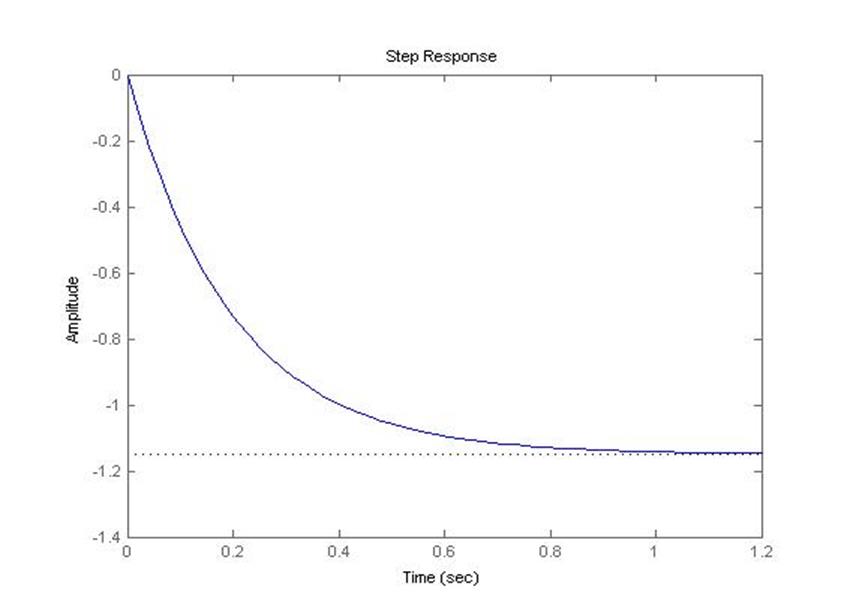
Процесс апериодический, tср=0.64 с

5. 2 Характеристики системы управления (2-й вариант)

K = -4.3549

S = 3.9359

E = -25.3764

Eigenvalue      Damping     Freq. (rad/s) 

 -3.08e-002     1.00e+000      3.08e-002

A =-25.3764               

Eigenvalue      Damping     Freq. (rad/s) 

 -2.54e+001     1.00e+000      2.54e+001   

5.2.1 Расположение полюсов самолета с системой управления

1) Разомкнутая система (без автопилота)

pzmap(raz)

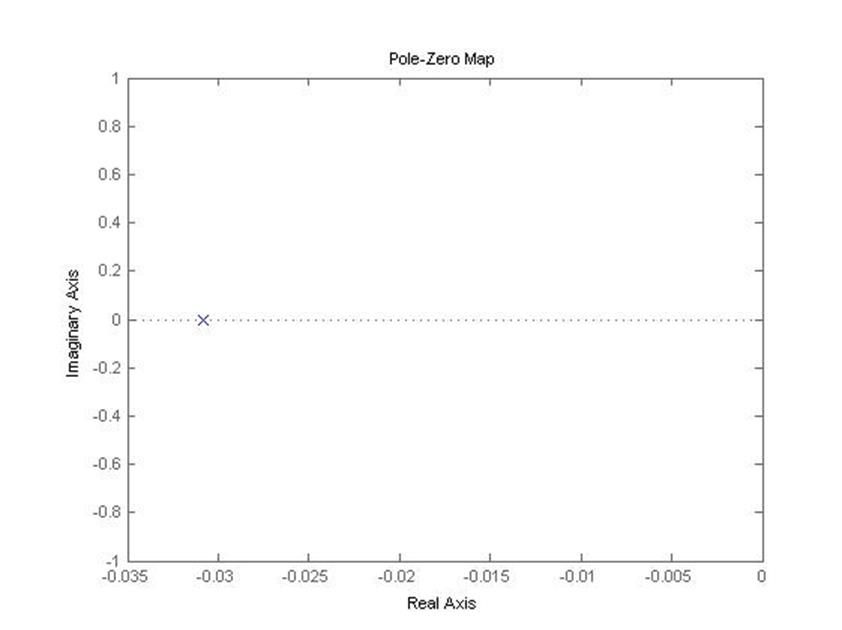
2) Замкнутая система (с автопилотом)

pzmap(zam)

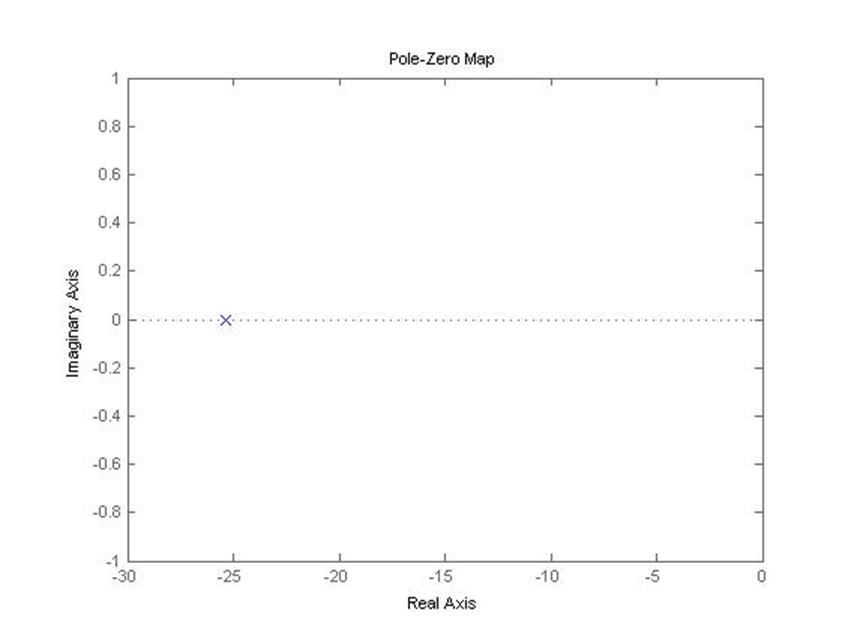
5.2.2 Логарифмические амплитудно-фазовые характеристики разомкнутой системы (самолет с автопилотом)

bode(raz)

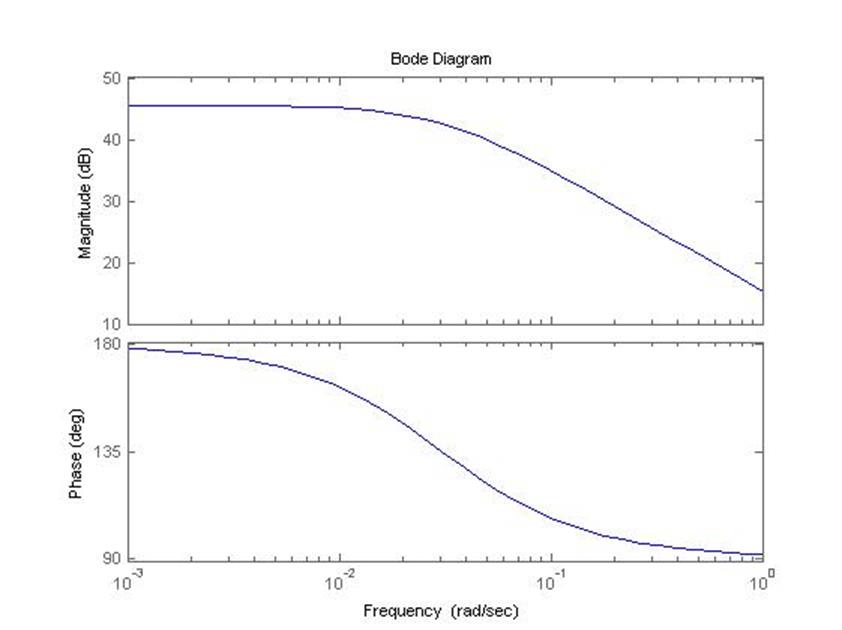
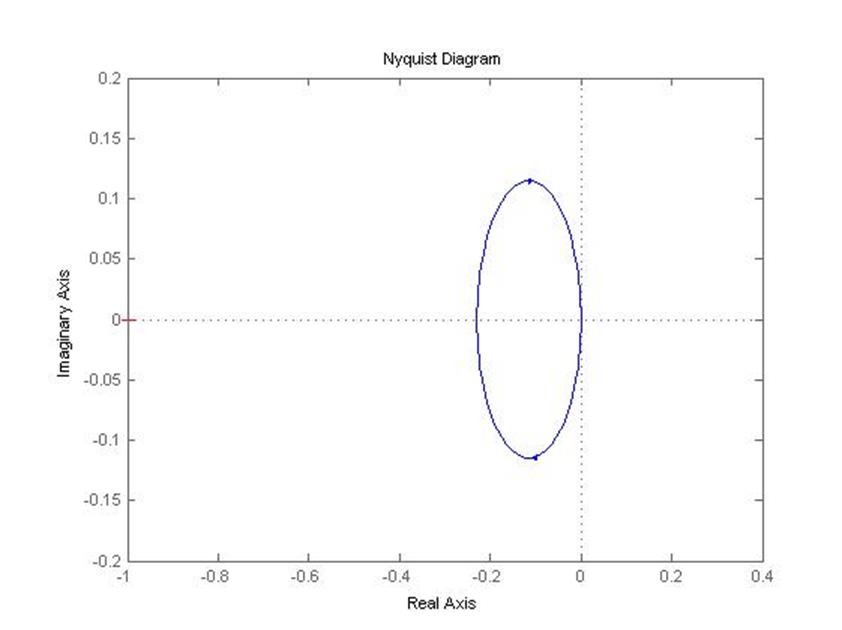
5.2.3 Годограф Найквиста замкнутой системы (самолет с автопилотом)

nyquist(zam)

5.2.4 Реакция замкнутой системы на ступенчатое отклонение (отклонение руля направления)

step(zam)

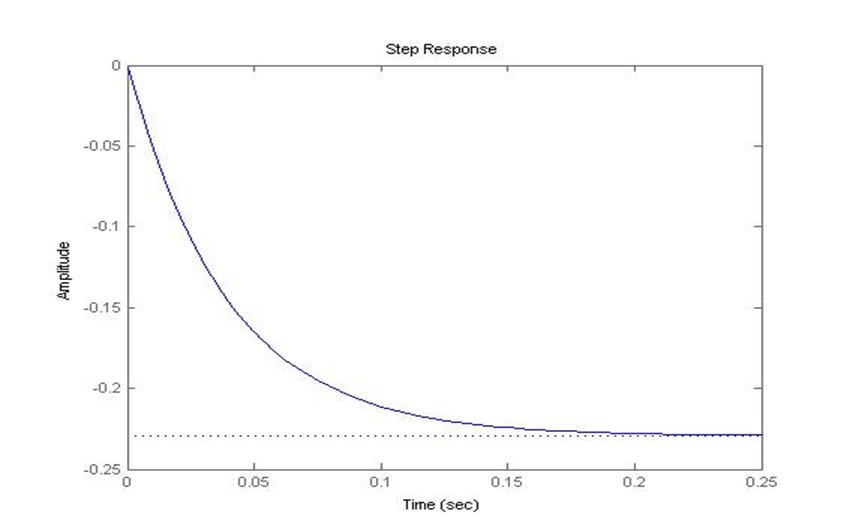
Процесс апериодический, tср=0,14 с

5. 3 Характеристики системы управления (3-й вариант)

K =-0.8266

S =0.7471

E =-4.8416

Eigenvalue      Damping     Freq. (rad/s) 

-3.08e-002     1.00e+000      3.08e-002   

A =-4.8416

Eigenvalue      Damping     Freq. (rad/s) 

 -4.84e+000     1.00e+000      4.84e+000  

5.3.1 Расположение полюсов самолета с системой управления

1) Разомкнутая система (без автопилота)

pzmap(raz)

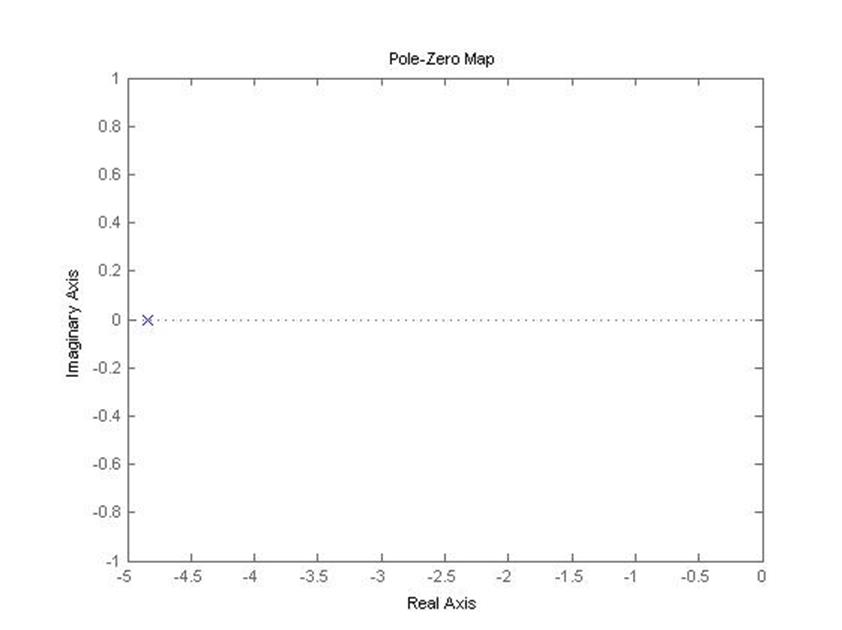
2)  Замкнутая система (с автопилотом)

pzmap(zam)

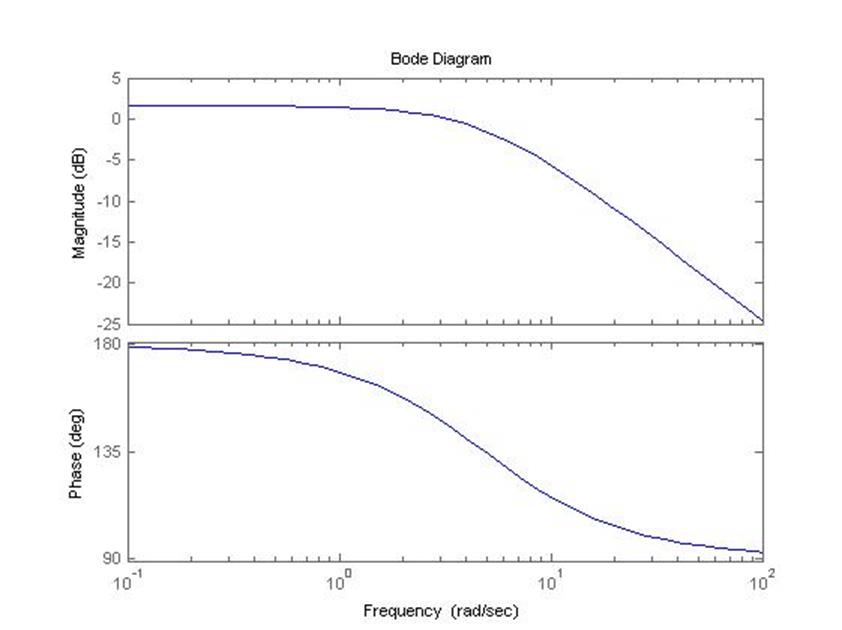
5.3.2 Логарифмические амплитудно-фазовые характеристики разомкнутой системы (самолет с автопилотом)

bode(raz)

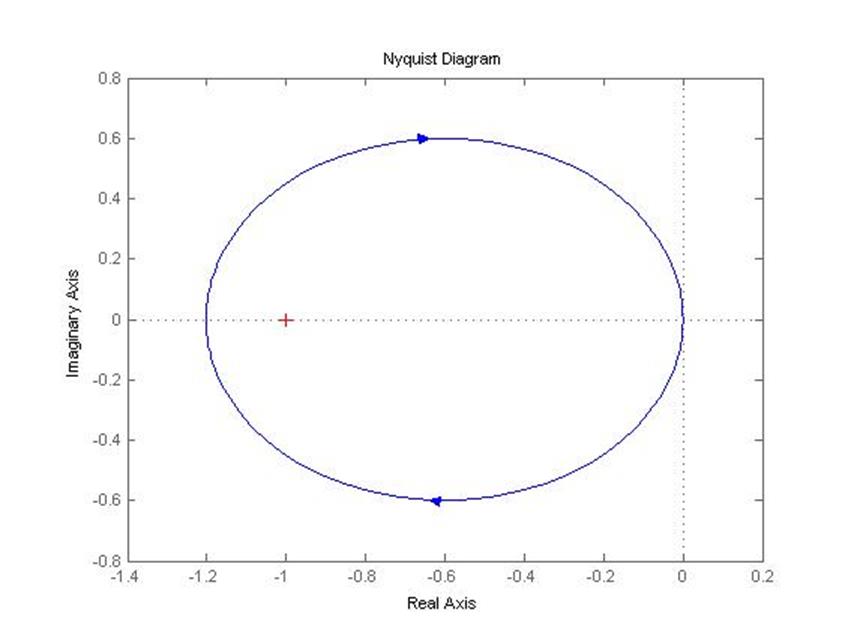
5.3.3 Годограф Найквиста замкнутой системы (самолет с автопилотом)

nyquist(zam)

       5.3.4 Реакция замкнутой системы на ступенчатое отклонение (отклонение руля направления)

step(zam)

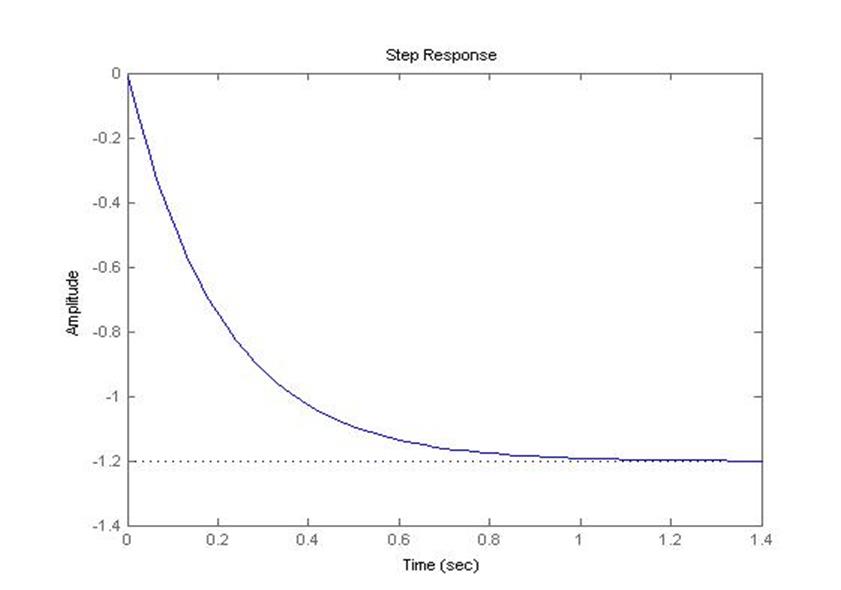
 Процесс апериодический, tcp=0.69 c

6. Сравнительный анализ систем управления.

Проводя сравнительный анализ трех вариантов весовых матриц, приходим к следующим выводам:

1)  Два из трех процессов (первый и третий) являются устойчивыми как в разомкнутом, так и в замкнутом состоянии.

Это видно из диаграммы полюсов (корни находятся в левой полуплоскости). Устойчивость замкнутой системы так же видно из ЛАФЧХ (в силу апериодичности процесса) и из годографа Найквиста.

Замыкая систему, мы увеличиваем степень устойчивости (на диаграмме полюсов полюс смещается влево).

Это нельзя сказать про второй процесс, так как на годографе Найквиста видно, что точка -1 не охватывается линией годографа.

2)  Все три процесса апериодические.

3)  Из полученных характеристик можно сделать вывод, что второй вариант подбора весовых коэффициентов не подходит, т.к. система становится неустойчивой в замкнутом состоянии. Наиболее быстродействующим из оставшихся является первый вариант.

Можно сделать вывод, что с увеличением разрешаемого отклонения рулевой поверхности увеличивается быстродействие, а с увеличением максимальной желаемой угловой скорости быстродействие падает.

Оптимальным следует считать первый вариант выбора коэффициентов, поскольку он обеспечивает хорошее быстродействие, малую максимальную угловую скорость и небольшие затраты отклонения рулевой поверхности. В третьем же варианте быстродействие не сильно хуже чем в первом, но на это требуются большие угловые скорости.

7. Текст программы

clc

close all

clear all

Ar = -0.0308;

B = -5.82;

F1 = 100;

G1 =5.26;

F=F1;

G=G1;

[K,S,E]=lqr(Ar,B,F,G)

C=eye(1);

D=0;

raz=ss(Ar,B,C,D);

damp(raz);

A=Ar-B*K

zam=ss(A,B,C,D);

damp(zam);

figure(1);

pzmap(raz);

figure(2);

pzmap(zam);

figure(3);

bode(raz);

figure(4);

nyquist(zam);

figure(5);

step(zam);

8. Список используемой литературы

 1) Конспект лекций по дисциплине «Управление движением ЛА». Н.И. Морозов

 2) Конспект лекций по дисциплине «Теория автоматического управления». Н.Н. Маркин

 3) Конспект лекций по дисциплине «Теория оптимального управления». Ю.В.Тюменцев