Синтез оптимального регулятора исследуемых параметров самолета БОИНГ-727

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

 

Московский Авиационный  Институт

(государственный технический   университет)

Кафедра 106

Динамики и управления летательных аппаратов.

Утверждено

руководитель

/Тюменцев Ю.В./

(подпись)

Защищено                                                                              

c оценкой

                 /                  /

    (дата)     (подпись)

Отчет о курсовой работе по курсу

«Теория оптимального управления»

____________

Тема: «Синтез оптимального регулятора исследуемых параметров самолета БОИНГ-727»

Выполнил студент группы 01-414

/Соколов В.М./

                                                                         (подпись)

                                                            Москва 2010 г.

Содержание.

§  1. Задание на курсовую работу ..................................................... 3

§  2. Исходные данные........................................................................ 4

§  3. Математическое описание продольного движения самолета                                                                                                               5

§  4. Вычисление матриц динамических коэффициентов......... 12

§  5. Синтез оптимального регулятора........................................... 13

§  6. Анализ характеристик рассматриваемой системы для разомкнутого и замкнутого случая............................................ 14

§  7. Исследование влияния вида оптимизирующего функционала на получаемое решение....................................... 20

§  8. Сравнительный анализ систем управления......................... 30

§  9. Текст программы....................................................................... 31

§  10.Список литературы.................................................................. 33

1.  Задание на курсовую работу

1. Разработать линеаризованную математическую модель возмущенного движения при управлении рулем направления.

2. Вычислить матрицы динамических коэффициентов и матрицы управления.

3. Для линеаризованной модели возмущенного движения самолета в канале курса с постоянной скоростью решить задачу АКОР.

4. Решить квадратичное матричное уравнение Риккати.

5. Вычислить коэффициенты усиления оптимального регулятора.

6. Вычислить собственные значения замкнутой системы с оптимальным регулятором.

7. Определить частоты и относительный коэффициент демпфирования разомкнутой и замкнутой системы управления.

8. Сравнить расположение полюсов разомкнутой и замкнутой системы управления.

9. Определить ЛАФЧХ замкнутой системы управления.

10. Определить характеристики переходного процесса для самолета с оптимальным регулятором.

2.  Исходные данные

Геометрические и физические характеристики

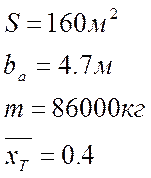
Стандартная атмосфера

                          

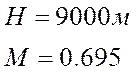
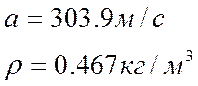
Аэродинамические характеристики

                                                             

                                        

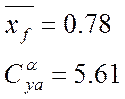
­­3.Математическое описание продольного движения самолета.

Уравнения движения самолета относительно инерциальной системы отсчета могут быть получены из основных теорем динамики твердого тела:

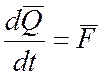
 и – главный вектор и главный момент относительно центра масс количества движения твердого тела (, );

 и   -  главный вектор и главный момент относительно центра масс внешних сил, действующих на твердое тело.

Если рассматривать самолет как твердое тело в произвольный момент времени, то к нему будут приложены: внешние силы, действующие на систему, сила тяги двигателя  и внутренние кориолисовые силы инерции:

      

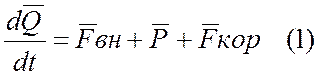
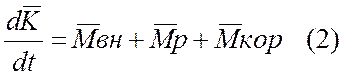
Удобнее исследовать движение самолета, пользуясь подвижными системами координат в начале с центром масс самолета. При проектировании производной по времени от какого-либо вектора  на оси любой подвижной системы координат OXYZ, вращающейся с угловой скоростью относительно выбранной системы отсчета (неподвижной), должны быть применены известные из векторного анализа формулы:

	(*)

 

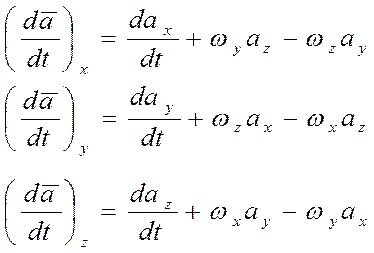
Пренебрегая скоростью и ускорением перемещения центра масс самолета относительно его корпуса, производная от количества движения по времени будет равна:

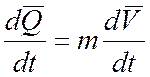
Учитываем правила векторного произведения  (*), разделяем полученные уравнения на проекции по осям XYZ, получим систему динамических уравнений движения в проекциях на оси системы координат, помещенных в центр масс самолета: