Математика \ Численные методы

Числове розв’язання нелінійних рівнянь. Відображення множин. Теореми про стискаючі відображення, страница 6

Застосовуючи формулу Тейлора, одержимо

0 = f(x)= f(xn) + f¢(xn)(x - xn)+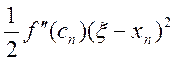,       (2.24)

де x<cn<xn. Оскільки f²(x)>0, маємо

  і отже, 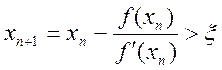, що і  потрібно було довести.

З огляду на знаки f(xn) та f¢(xn), маємо xn+1<xn (n=0,1,…), тобто послідовні наближення x0,x1,…,xn,…утворять обмежену монотонно спадну послідовність. Отже, існує .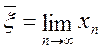

Переходячи до границі в рівності (2.22), будемо мати

 ,

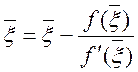тобто f()= 0. Звідси =x, що і потрібно було  довести.

Тому, застосовуючи метод Ньютона, варто керуватися таким правилом: за вихідну точку x0  вибирається той кінець інтервалу (а,b), якому відповідає ордината того самого знака, що і знак f²(x).

Зауваження. З формули (2.22) бачимо, що чим більше числове значенняf¢(x) в околі кореня, тим меншою є поправка, яку треба додати до попереднього наближення, щоб отримати наступне. З цієї причини метод Ньютона особливо зручний тоді, коли в околі кореня графік функції має велику крутизну. Якщо ж f¢(x) біля кореня – мала, то застосовувати даний метод не рекомендується.

Для оцінки похибки n-го наближення xn можна скористатися  формулою 

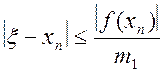 ,                    (2.25)

де m1 найменше значення ½f¢(x)½ на відрізку [a,b].

Виведемо ще одну формулу для оцінки точності наближення xn.

Застосовуючи формулу Тейлора, маємо:

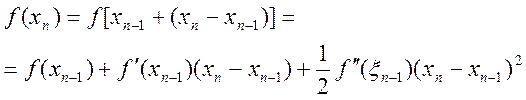 , (2.26)

де  xn-1Î (xn-1, xn). Оскільки з визначення наближення xn маємо

, то з (2.26) знаходимо: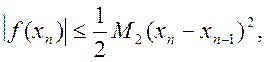 де М2 – найбільше значення ½f² (x)½ на відрізку [a,b]. Отже, на підставі формули (26) остаточно одержуємо

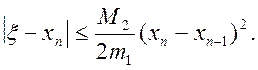              (2.27)

Якщо процес збігається, то xn-xn-1 ®0 при n®¥. Тому при n³N маємо  тобто «усталені» початкові десяткові знаки наближень xn-1 і xn, починаючи з деякого наближення, є правильними.

Зауважимо, що в загальному випадку збіг з точністю до eдвох послідовних наближень xn-1 і xn зовсім не гарантує, що з тією самою точністю збігаються значення xn і точний корінь x.

Проаналізуємо абсолютні похибки двох послідовних наближень xn і xn+1. З формули (2.24) одержуємо

 ,

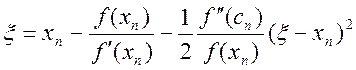де cnÎ(xn,x). Звідси, з огляду на формулу (2.22), будемо мати

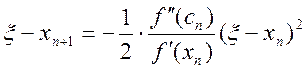
і, отже,

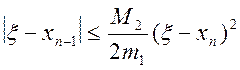.                 (2.28)

Формула (2.28) забезпечує швидку збіжність процесу Ньютона, якщо початкове наближення x0 таке, що 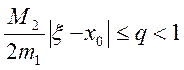. Зокрема, якщо  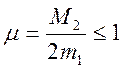і , тобто наближення xn мало m правильних десяткових знаків після коми, то наступне наближення xn+1 буде мати не менше 2m правильних знаків; іншими словами, якщо , то за допомогою методу Ньютона число правильних знаків після коми шуканого кореня x подвоюється на кожному кроці.

Приклад. Знайти корінь рівняння  з точністю

  1 Це рівняння має один корінь на (f(0)f(1))<0)

Знайдемо похідні

  .

  2 Вибираємо початкове наближення кореня  так, щоб  Обираємо , тому що .

3  Будуємо ітераційну  послідовність

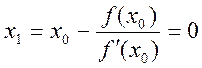
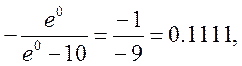
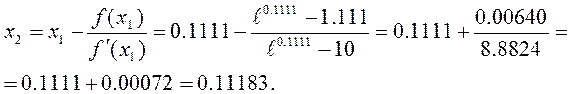                       4 Обчислення припиняємо , тому що , і за наближене значення кореня з точністю  беремо

Приклад реалізації чисельного алгоритму розв’язування нелінійних рівнянь на псевдокоді

//Метод Ньютона. Вважаємо, що умова збіжності методу перевірена

f(x):

   //повертає значення функції для даного х

end

f1(x):

 //повертає значення першої похідної функції для данного х

end

f2(x):

  //повертає значення другої похідної функції для даного х

end

//a,b – границі відрізка, eps – точність розв’язку

Solve_Nonlinear(a,b,eps):      

1  if f1(a)<f1(b) then

2   min:=abs(f1(a))

3  else

4   min:=abs(f1(b))

5  fi

6  if f2(a)>f2(b) then

7   max:=abs(f2(a))

8  else

9   max:=abs(f2(b))

10  fi

11  fault:=sqrt(2*min*eps)

12  if f(b)*f2(b)>0 then

13   x:=b

14  else

15   x:=a

16  fi

17  repeat

18   n++

19   if n>1 then

20   x:=xn

21   fi

22   xn:=x-f(x)/f1(x)

23  until abs(xn-x)<=fault

24  return x

end

2.8 Обумовленість задачі визначення кореня

Скачать файл