Математика \ Численные методы

Числове розв’язання нелінійних рівнянь. Відображення множин. Теореми про стискаючі відображення, страница 5

Для оцінки наближення можна дати іншу формулу, корисну в деяких випадках. Представимо f(x)=x-j(x).

Очевидно, що  Звідси, з огляду на те, що f(x)=0, одержимо:

де , і, отже,

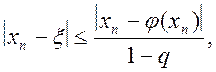                                              (2.19)

тобто

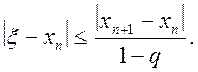                                 (2.20)

Використовуючи формулу (2.12), маємо також

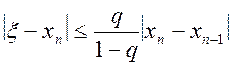                       .            (2.21)

Звідси, зокрема, випливає, що якщо q£ , то . В цьому випадку з нерівності  випливає нерівність* .

Зауваження. Існує поширена думка, що якщо при застосуванні методу ітерації два послідовні наближення xn-1 і xn збігаються між собою із заданою точністю e (наприклад, для цих наближень установилися т перших десяткових знаків), то з тією самою точністю справедлива рівність x» xn (тобто, зокрема, у наведеному прикладі т знаків наближеного числа xn є правильними!). У загальному випадку  це твердження помилкове. Більше того, легко показати, що якщо j'(х) близька до 1, то величина |x- xn| може бути великою, хоча  |xn - xn-1| дуже мала.

Формула (2.20) дає можливість оцінити похибку наближеного значення xn за різницею двох послідовних наближень xn-1 і xn.

Процес ітерації варто продовжувати доти, поки для двох послідовних наближень xn-1 і xn не буде забезпечене виконання нерівності

,

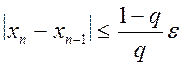де e - задана гранична абсолютна похибка кореня x і ½j¢(x)½ £ q. Тоді за формулою (2.21) будемо мати  нерівність , тобто x = xn ±e.

  Зауважимо, що якщо xn=j(xn-1) і *=j(), то ,, тобто  .

Таким чином, при ітераційному процесі, що збігається, похибка прямує до нуля монотонно, тобто кожне наступне значення xn є більш точним, ніж попереднє значення хn-1. Як правило, при всіх цих висновках ігноруються похибки округлень, тобто передбачається, що послідовні наближення знаходяться точно.

На практиці здебільшого буває так, що грубим прийомом встановлюється існування кореня рівняння (2.7) і методом ітерації потрібно одержати досить точне наближене значення кореня, причому нерівність (2.9) виконується лише в деякому околі (a, b) цього кореня. Тут при невдалому виборі початкового значення x0 послідовні наближення xn=j( xn-1) (n = 1,2,…) можуть залишити інтервал (a, b) чи навіть втратити сенс.

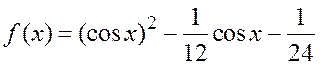  Приклад. Розв’язати рівняння f(x)=0 на заданому відрізку  [a,b]=[0, ], де =0,   

Аналітичне розв’язання задачі. Розкладемо функцію 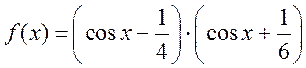.  Точні значення коренів 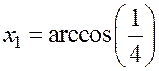=1.31811607652818,  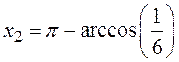 =1.738244406014586.

Чисельне розв’язання задачі. Локалізація кореня для чисельного розв’язання задачі

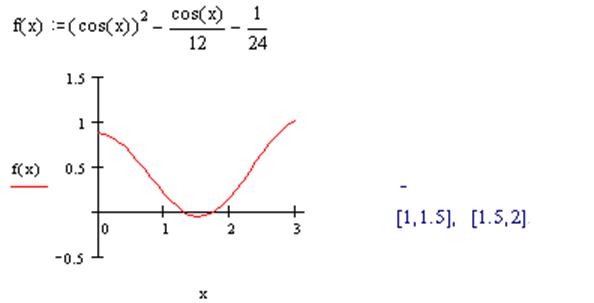Метод бісекції, зреалізований у пакеті Mathcad, дає

Перший  корінь

bisec.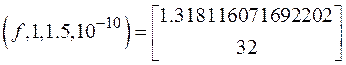

  Обравши - задання початкового наближення, користуємось убудованою функцією пакета MATHCAD

.

  Значення  кореня відрізняється від знайденого за допомогою функції  bisec , тому що за замовчуванням величина похибки при роботі вбудованих функцій дорівнює  0.001.

  Перевизначимо параметр для задання похибки

.

  Значення кореня із заданою точністю  1.3181160717.

Другий  корінь

bisec.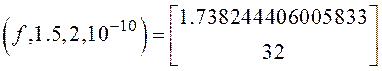

Значення кореня із заданою точністю  1.7382444060,  число ітерацій  32; - задання початкового наближення;   .

Значення кореня  у межах заданої точності збігаються.

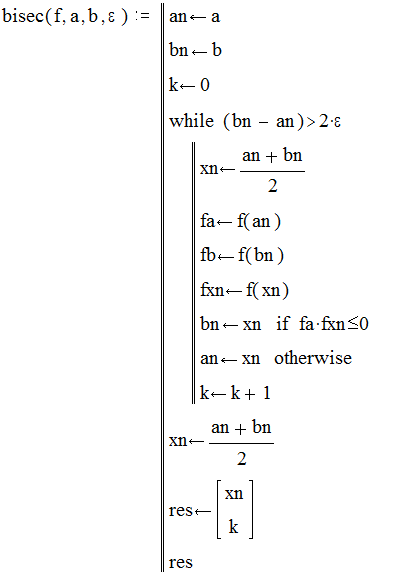
2.7 Метод Ньютона

Метод Ньютона (метод дотичних) для наближеного розв’язку рівняння  полягає в побудові ітераційної послідовності

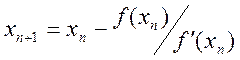,                   (2.22)

що збігається до кореня рівняння, на відрізку  локалізації кореня.

Теорема 7 Якщо f(a) f(b)<0, причому f¢(x) і f²(x) не дорівнюють нулю і зберігають певні знаки при a £ x £ b, то, виходячи з початкового наближення x0Î[a,b], що задовольняє нерівність

,                           (2.23)

можна обчислити методом Ньютона єдиний корінь x рівняння  з будь-яким ступенем точності.

Доведення. Нехай, наприклад, f(а)<0,  f(b)>0, f¢(x)>0, f²(x)>0 при a £ x £b (інші випадки розглядаються аналогічно). Відповідно до нерівності (2.23) маємо f(x0)>0. (наприклад, можна взяти x0=b). Методом математичної індукції доведемо, що всі наближення xn>x (n=0,1,2…) і, отже, f(xn)>0. Справді, насамперед, x0>x. Нехай тепер xn>x. Покладемо x = xn + (x - xn).

Скачать файл