Числове розв’язання нелінійних рівнянь. Відображення множин. Теореми про стискаючі відображення, страница 4

4a Якщо знаки f_a і f₀ різні, то вважати корінь обмеженим на [a,x₀] -> вихід.

4b Якщо знаки f_b і f₀ відрізняються, то вважати корінь обмеженим на [x₀,b] -> вихід.

5 Перевіряється, яке з f_a і f_b найменше. Якщо  вони однакові, то переходимо до 6a (двосторонній пошук), якщо f_b – робимо пошук вправо 6b, інакше - пошук уліво 6c.

 6a Знаходимо a=a-D, b=b+D, f_a=f(a), f_b=f(b), йдемо до пункту 3.

         6b Присвоюємо послідовно a=x₀, x₀=b, f_a=f₀, f₀=f_b; знаходимо b=b+D, f_b=f(b), йдемо до пункту 3.

 6c. Аналогічно 6b, тільки напрямок пошуку -  вліво.

2.6 Метод простих ітерацій

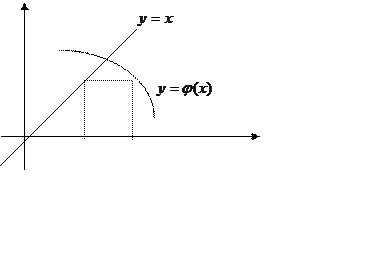Замінимо рівняння  еквівалентним йому рівнянням .

                          y

 

                      O       a   x₁  x^*    x₀  b                       x

Рисунок 2.2

Виберемо деяке наближення  кореня і підставимо його в праву частину. Одержимо . Далі обчислюємо за формулами: . Отримуємо послідовність наближень {} до кореня, що у випадку її збіжності до кореня  може дати наближене його значення із заданою точністю .

Теорема 6 Нехай функція j(x) визначена і диференційована  на відрізку [a,b], причому всі значення j(х)Î [a,b] .Тоді якщо існує правильний дріб  q,  такий,  що

             ½j^¢(x)½£ q <1                    (2.9)

при a<x<b, то:  процес ітерації

                           x_n=j(x_n-1)     (n = 1,2,…)(2.10)

1)  збігається незалежно від початкового значення x₀Î[a,b];

2)  граничне значення  є єдиним коренем рівняння                                  x=j(x)                               (2.11)

на відрізку  [a,b].     

Доведення. Розглянемо два послідовних наближення x_n=j(x_n-1) і x_n+1=j(x_n)  (які внаслідок умов теореми існують). Звідси  x_n+1 -  x_n= j(x_n) - j(x_n-1).

Застосовуючи теорему Лагранжа, будемо мати:

x_n+1 -  x_n  = (x_n - x_n-1) j^¢(), де  .

Отже, на підставі умови (2.9) одержимо

                     (2.12)

Звідси, надаючи значення n=1,2,3,…, отримаємо:

;

            

                ..............................................

                 (2.13)

  Розглянемо ряд:

      x₀ + (x₁- x₀) + (x₂- x₁) + … + (x_n – x_n-1) + … ,      (2.14)

для якого наші послідовні наближення x_n є (n+1)-ми частковими сумами, тобто x_n=S_n+1. За нерівністю (2.13) члени ряду (2.14) за абсолютною величиною менші відповідних  членів геометричної прогресії зі знаменником q<1, тому ряд (2.14) збігається, до того ж абсолютно. Отже, існує 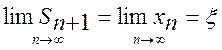, причому, вочевидь, Î[a,b]. Переходячи до границі в рівності (2.10), зважаючи на неперервність функції j(x) одержуємо

       =j( ).                              (2.15)

  У такий спосіб  є корінь рівняння (2.11). Іншого кореня на відрізку [a,b] рівняння (2.11) не має. Дійсно, якщо

                        ,                               (2.16)

то з рівностей (2.15) і (2.16) одержимо

і отже,                     ,                        (2.17)

де c Î. Оскільки вираз у квадратній дужці в рівності (2.17) не дорівнює нулю, то , тобто корінь  - єдиний.

Зауваження 1 Теорема залишається правильною, якщо функція j(x) визначена і диференційована на інтервалі , причому при x Î (-¥;+¥) виконана нерівність (2.9).

Зауваження 2 В умовах теореми метод ітерації збігається при будь-якому виборі початкового значення x₀  Î[a,b]. Завдяки цьому він є  самовиправним, тобто окрема помилка в обчисленнях, що не виводить за межі відрізка [a,b,] не вплине на кінцевий результат, тому що помилкове значення можна розглядати як нове початкове значення x₀. Можливо, зросте лише обсяг роботи . Властивість самовиправлення робить метод ітерації одним із найнадійніших методів обчислень.

Оцінка наближення. З формули (2.13) маємо:

Застосувавши формулу суми геометричної прогресії, одержимо:

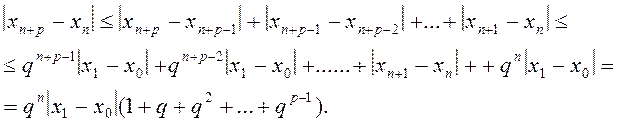
Спрямовуючи число р до нескінченності і з огляду на те, що 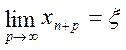, знаходимо остаточно:

                             .                (2.18)

Звідси ясно, що збіжність процесу ітерації буде тим швидшою, чим менше число q.