хn = j (хn-1), n > 1.
Викладений у теоремі метод побудови нерухомої точки називається методом простих ітерацій або методом послідовних наближень, а послідовність {хn} — ітераційною послідовністю.
2.3 Теореми про стискаючі відображення
Розглянемо повний метричний простір Х з відстанню r. Відображення f: X®Xназивається стискаючим, якщо існує таке число q є (0, 1), що
(2.4)
для всіх елементів х1, х2 є X.
Має місце наступне узагальнення теореми 3.
Теорема 4 (про стискаючі відображення). Стискаюче відображення f: X®X має єдину нерухому точку х* є X, яку можна знайти як границю послідовності
(2.5)
де х0 — довільний елемент із X. Крім того виконується
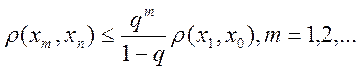(2.6)
Доведення. Покажемо, що послідовність {хn} фундаментальна. З (2.4) і (2.5) одержуємо оцінки
Вважаючи для визначеності, що n>m, з нерівності трикутника одержуємо оцінки
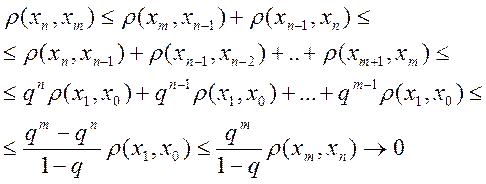
при m®∞.
Таким чином, побудована послідовність {хn} фундаментальна. Оскільки метричний простір X повний, то вона має границю х* є X. Оскільки
то при n®∞ з наведених оцінок одержуємо доведену оцінку (2.6). Оскільки при m®∞
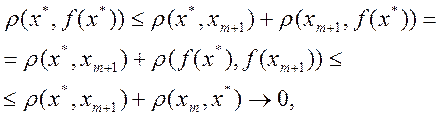
то f(x)= x* , тобто x* — нерухома точка відображення f.
Доведемо, що вона — єдина. Нехай x** — інша нерухома точка для f. Тоді з оцінки
випливає, що r( x*, x**) = 0 і тому x* = x**.
Теорема доведена.
Нерівність (2.6) дозволяє визначити, скільки потрібно знайти послідовних наближень, щоб знайти нерухому точку x* відображення f із заданою точністю e>0. Наприклад, нерівність r( x*, хm) <eбуде виконана, якщо
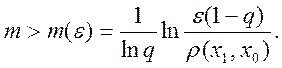
Теорема 4 широко застосовується для пошуку розв’язків систем алгебраїчних, диференціальних та інтегральних рівнянь, а також покладена в основу різних методів, які використовуються в обчислювальній математиці.
2.4 Критерій існування нерухомих точок
Розглянемо узагальнення теорем 1 і 2, що пов'язані з питаннями існування нерухомих точок відображень. Формулювання відповідних результатів використовує наступні важливі поняття.
Множина К з метричного простору X, на якому введена відстань r, називається компактною, якщо з будь-якої послідовності {хn} елементів цієї множини можна виділити підпослідовність, що збігається, границя якої також належить К.
Множина В з лінійного простору X (тобто
множина, на якій визначені операції додавання і множення на числа з R)
називається опуклою, якщо разом з будь-якими двома точками х1, х2єВ
множині В належать усі точки ах1+(1-а)х2, а
[0,1] (множина таких точок
називається відрізком, що з'єднує точки х1, x2єВ).
Теорема 5. Будь-яке неперервне відображення f: К®К опуклої компактної множини К з лінійного простору Rn має нерухому точку.
Ця теорема доведена голландським математиком Л.Э.Я. Брауером. Оскільки будь-який відрізок [а, b] з R є опуклою компактною множиною, то теорема 2 випливає з теореми Брауера. Розглянемо деякі наслідки теореми 5.
Теорема Бореука-Улама для кола. Нехай f: С®R — функція на колі С. Тоді існує пара точок-антиподів х, х* така, що f(х) =f(x*).
Наслідком цієї теореми є той факт, що на будь-якому колі Земної кулі (наприклад, на екваторі) знайдеться пара
антиподів, у яких температура повітря однакова.
Теорема (про млинці). Якщо А і В — обмежені фігури на площині, то існує пряма, що поділяє кожну з цих фігур на дві рівновеликі за площею частини.
Тут передбачається, що кожна фігура має площу (що може бути тоді, коли фігура має складну форму). Образно кажучи, теорема стверджує, що два млинці, що лежать на тарілці, можна розрізати точно навпіл одним змахом ножа.
Теорема Брауера має різноманітні узагальнення, що знаходять застосування в питаннях існування розв’язків диференціальних та інтегральних рівнянь, у математичній економіці (теорія економічної рівноваги) і теорії ігор.
Нехай задана функція f(х) дійсної змінної. Потрібно знайти нулі функції f(х) або, що те ж саме, корені рівняння
f(x)=0 (2.7)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.