Теорія прийняття рішень. Механізм прийняття рішень. Особливості реалізації механізму прийняття рішень на ЕОМ, страница 9

Рис. 5. Залежність ентропійного критерію (3.2.2) від точнісних характеристик (М=2)

Як видно з рис. 5, функція критерію є взаємно-неоднозначною. Тобто вона приймає два максимуми, перший у випадку, коли D₁  та D₂  приймають значення 1, а другий, коли D₁  та D₂ приймають значення 0. В першому випадкові максимум достовірностей свідчить про те, що отримано безпомилковий за навчальною матрицею контейнер(всі реалізації свого класу потрапили в контейнер, жодна реалізація чужого класу не потрапила в поточний контейнер)-тобто в такому випадкові контейнер має максимум інформації по відношенню до класа-сусіда, у другому ж випадкові, нульові значення першої та другої достовірності свідчать про те, що контейнер поточного класу взагалі не відрізняється від класа-сусіда.

Отже перший випадок - це критерій максимальної різноманітності.

Другий випадок-критерій максимальної схожості.

Оскільки нам необхідно знайти максимум різноманітності, то ми розбиваємо навпіл область визначення функції інформаційного критерію. Будемо шукати максимум Е в області для , котру ми будемо називати робочою областю визначення інформаційного критерію.

Тоді, врахувавши всі особливості, отримаємо такий алгоритм розрахунку оптимальних радіусів:

1. Обрати поточний клас.

2.Для кожного класу перебирається радіус від 1 до певного заданого числа(в загальному випадкові-до - кількості ознак).

3.При і-тому значенні радіусу будується контейнер. Розраховуються точні сні характеристики.

4. Точнісні характеристики підставляються в функцію

5.Серед значень Е, котрі знаходяться в робочій області (тобто при тих значеннях радіусу, для котрого ) обирається максимальне. Воно відповідає певному радіусу. Отже, контейнер з таким радіусом відповідає принципу максимальної різноманітності.

7.Реалізація алгоритму екзамену – алгоритму прийняття рішення.

Процес створення системи прийняття рішення складається з двох етапів-навчання та екзамен.

Навчання-це процес створення досвіду, в той час як екзамен - реалізація визначення належності поточного стану до того чи іншого класу розпізнавання.

Належність реалізації до того чи іншого контейнеру означає те, що параметри поточного стану об’єкта є найбільш схожими з типовими характеристиками перебування об’єкта в певному стані.

Належність поточної реалізації визначається за допомогою функції належності-виразу, що чисельно інтерпретує ступінь належності екзаменаційної реалізації до того чи іншого контейнера.

Прикладом функції належності може бути вираз:

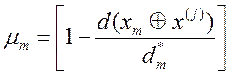
Тут значення функції належності до m-того класу розпізнавання(стану об’єкту),

В чисельнику виразу знаходиться кодова відстань від екзаменаційної реалізації до еталонного вектора m-того класу, в знаменнику-оптимальний радіус контейнера m- того класу.

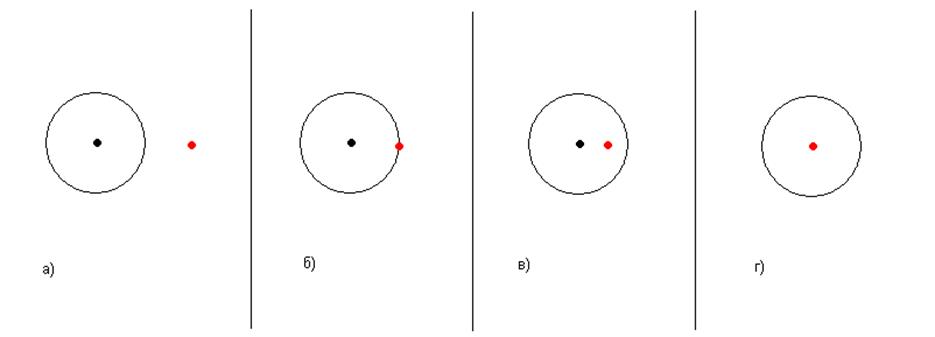
В результаті можна отримати наступні значення функції належності в залежності від позиції реалізації( На рисунку 6 зображено характерні ситуації положення реалізації відносно контейнера. Реалізація позначена червоним кольором, а контейнер - чорним )

1) Реалізація знаходиться поза контейнером(Рис 6.а)-тоді <0.

2) Реалізація знаходиться на межі контейнера(Рис 6.б)-тоді =0.

3) Реалізація знаходиться в  контейнері (Рис 6.в)-тоді .

4) Реалізація знаходиться в центрі контейнера (Рис 6.г)-тоді <1.

Алгоритм визначення належності поточної екзаменаційної реалізації до того и іншого класу розпізнавання визначається за алгоритмом:

1.  Сформувати екзаменаційну вектор-реалізацію.

2.  Бінеаризувати екзаменаційну вектор-реалізацію за допомогою системи контрольних допусків, отриманої на другому етапі алгоритму навчання.

3.   Розрахувати функції належності екз. реалізації до контейнерів всіх класів розпізнавання.

4.  За значеннями функцій належності прийняти рішення :

4.1  Всі значення функцій належності від’ємні прийняти рішення про неналежність поточної вектор-реалізації до жодного з класів.

4.2  Серед значень функцій належності є додатні-прийняти рішення про належність екз. реалізації до класу, значення належності до котрого(серед додатних) є максимальним.