Теорія прийняття рішень. Механізм прийняття рішень. Особливості реалізації механізму прийняття рішень на ЕОМ, страница 6

Отже обраний нами критерій для знаходження радіусу не є універсальним. Що ж є більш універсальним принципом  для подібного роду задач?

Відповідь одна-інформаційні критерії, що пояснюють міру різноманітності отриманих образів по відношенню один до одного. Адже інформація є найбільш універсальною сутністю, здатною описати різноманітні відношення між об’єктами. Нас же найбільше цікавить, наскільки вони будуть відрізнятися один від одного, адже при цьому достовірність правильного прийняття рішення буде більшою по відношенню до ситуації, коли різноманітність буде меншою а отже може мати місце перетин між контейнерами класів.

В такому випадкові використовувати інформаційний критерій – значить підбирати  параметри контейнера  таким чином,  щоб отриманий контейнер містив якомога більше інформації про свої реалізації та якомога менше про чужі.

Тому можна використовувати критерії що  відображають інформаційні характеристики розподілу і пояснюються або виражаються дистанційними характеристиками, наприклад близькістю точок, геометричними ймовірностями потрапляння тих чи інших точок у той чи інший контейнер.

В нашому випадкові досягти максимуму даного контейнера-значить досягти максимальної різноманітності між контейнерами отриманих образів.

Для того щоб оперувати поняттями інформаційного критерію, треба дозволити самій же ЕОМ краще оцінювати міру схожості та різноманітності реалізацій класів розпізнавання.

Одним з можливих способів досягти поставленої мети-це переведення реалізацій в бінарний простір, де відстанню між ними буде кількість неспівпадінь по їх компонентам, котру будемо називати відстанню Хеммінга, кодовою відстанню, або ж кодовою відстанню Хеммінга.

Процедура переведення полягає у знаходженні контрольних допусків , що задають певний інтервал в області нормованих(експлуатаційних, робочих) допусків ознак розпізнавання , при цьому належність значення ознаки до інтервалу означає еквівалентність її значенню «1» в бінарному просторі, та «0» за умови, якщо ознака не потрапила до коридору контрольних допусків. Система контрольних допусків-це набір пар у вигляді верхнього та

нижнього контрольного допуску для кожної ознаки розпізнавання. Вони формуються по значенням ознак одного класу,  а застосовуються для значень ознак всіх класів.

Алгоритм бінеаризації навчальної матриці наступний:

1.  Обрати базовий клас, або клас по реалізаціям котрого будуть розраховуватися контрольні допуски.

Наприклад , нехай  - базовий клас.

2.  Розрахувати вектор середніх значень по ознакам базового класу.

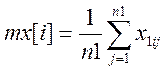
3.  обрати параметр – ширина інтервалу.

4.  Розрахувати контрольні допуски, за алгоритмом:

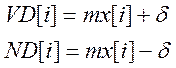
5.  Провести бінеарізацію за алгоритмом:

3.Розрахунок еталонних векторів (центрів), контейнерів класів розпізнавання.

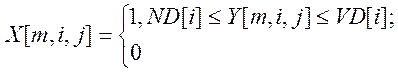
Як ми пам’ятаємо, метою навчання СППР є побудова контейнерів, що описують характерні параметри перебування об’єкту керування в тому чи іншому стані. Знайти радіус та контейнер для навчальних матриць всіх класів-значить отримати вирішальне правило, а отже виконати навчання системи підтримки прийняття рішень.

Радіус, або ж центр наших контейнерів логічно розміщувати в точці найбільшої концентрації реалізацій. Тому усереднивши наприклад всі реалізації одного класу, ми отримаємо реалізацію, що співпадає з центром розподілу всіх реалізацій. Таку реалізацію будемо називати еталонним вектором, оскільки вона містить середньостатистичні характерні значення параметрів реалізацій, отже відбиває типові характеристики перебування об’єкта в даному стані . Параметри  еталонного вектора повністю підходять для того, виконувати роль центра утворюваного контейнера.