Теорія прийняття рішень. Механізм прийняття рішень. Особливості реалізації механізму прийняття рішень на ЕОМ, страница 7

Але є одна особливість, викликана технічними умовами. Оскільки процес розрахунку еталонного вектора для кожної навчальної матриці полягає в вирахуванні середнього арифметичного по ознакам, в результаті виконання такої операції може виникати число, що не належить до бінарного простору(тобто не 0 та не 1,  щось між ними, наприклад 0,8). Оскільки еталонний вектор, так як і інші реалізації класів розпізнавання, лежить у бінарному просторі, та повинен приймати значення 0 або 1, використовується правило приведення розрахованого середнього значення до бінарного виду шляхом порівняння(квантування) з деяким коефіцієнтом, котрий має назву «рівень селекції» та позначається літерою  .

Тоді алгоритм розрахунку еталонних векторів для класів розпізнавання є наступним:

1.Ввести рівень селекції (по замовчуванню 0,5).

 - рівень селекції.

2. Розрахувати середні значення(частоти) ознак класів розпізнавання шляхом усереднення навчальних матриць по стовпцям.

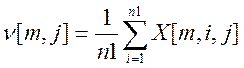
3.Розрахувати еталонний вектор за правилом.

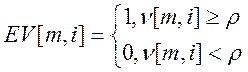
Наступним етапом навчання є визначення радіусів контейнерів.

В пункті 2 було описано можливі ситуації розміщення реалізацій, їх можливий перетин. Також було сказано, що використання інформаційного критерію дозволяє підібрати параметри контейнера таким чином, щоб вони містили максимум інформації про поведінку того чи іншого об’єкта. Введемо поняття критерію максимальної різноманітності –це критерій, функція котрого досягне максимуму у випадку, коли в отриманий контейнер буде входити максимум своїх реалізацій та мінімум чужих.

Тоді у  випадку, коли класи  не  перетинаються, можна брати в якості радіусу відстань до найбільш віддаленого елемента (в контейнер в такому випадку потраплять всі інформаційні носії-реалізації, і жодна з реалізацій іншого класу не потрапить до нього). У випадку ж, коли класи перетинаються, буде обрано саме таке значення радіусу, при котрому отриманий контейнер відповідає максимальній різноманітності.

Розглянемо в якості інформаційного критерію статистичні міри Шеннона на Кульбака.

Це є функції , параметрами котрих є точні сні характеристики-параметри за допомогою котрих можна оцінити якість отриманих контейнерів.

К₁-кількість своїх реалізацій, що потрапили в контейнер

К₂-кількість своїх реалізацій, що не потрапили в контейнер

К₃-кількість чужих реалізацій, що потрапили в контейнер

К₄-кількість чужих реалізацій, що потрапили в контейнер

Як ми бачимо, точні сні характеристики залежать від того, який радіус для поточного контейнера  ми оберемо.

Фактично, процес розрахунку оптимального радіусу є наступним:

1.Для кожного класу перебирається радіус від 1 до певного заданого числа.

2.При і-тому значенні радіусу будується контейнер. Розраховуються точні сні характеристики.

3. Точнісні характеристики підставляються в функцію

4.Серед значень Е обирається максимальне. Воно відповідає певному радіусу. Отже, контейнер з таким радіусом відповідає принципу максимальної різноманітності.

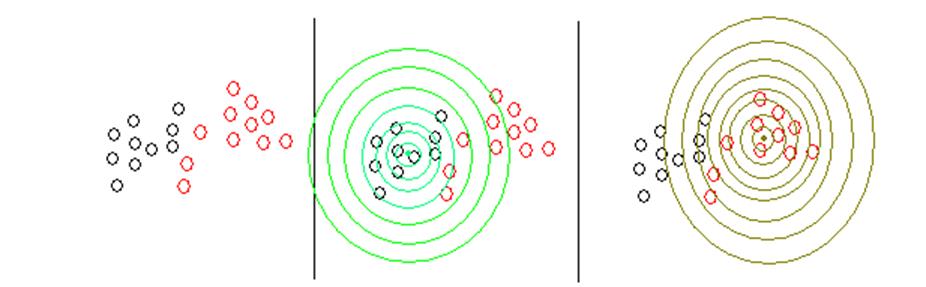
На рисунку 3 ілюстровано процес вибору оптимальних радіусів для контейнерів двох класів розпізнавання,  на реалізації котрого накладено гіпотезу апріорної нечіткої компактності.

В наступних пунктах ми будемо розглядати деталі процесу розрахунку оптимальних радіусів.

4.Розрахунок масиву PARA.

Отже переходимо до розрахунку радіусів контейнерів. Нехай у нас задано три класи. Обираємо конкретний клас.

Починаємо перебирати радіус від 1 до наприклад максимально можливого значення-кількості ознак.

Пробуємо розрахувати точнісні характеристики для конкретного радіуса.

На рисунку 4 показано розподіл реалізацій трьох класів. Наприклад, ми починаємо для червоного  класу виконувати кроки по знаходженню оптимального радіусу.

Але виникає питання-що вважати реалізаціями чужого класу? Адже у нас два класи можуть претендувати на цю роль, а точні сні характеристики повинні змінюватися від 0 до , де - кількість реалізацій. Логічно обрати в якості чужих реалізацій ті, котрі найбільш суттєво впливають на якість отриманого вирішального правила, тобто ті, що найбільше заважають побудувати оптимальний контейнер.