



СУМСЬКИЙ ДЕРЖАВНИЙ УНІВЕРСИТЕТ
КАФЕДРА ІНФОРМАТИКИ
Звіт з лабораторної роботи №8
на тему:
“Чисельні методи розв’язання звичайних диференціальних рівнянь ”
з дисципліни:
Карчов Валерій
Використовуючи
метод прогнозу і корекції, розв’язати крайову задачу для
звичайного диференціального рівняння з точністю ![]()
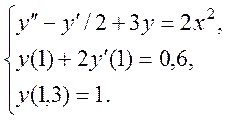
Нехай ![]() та
та ![]() . Тоді задана система
прийме вигляд:
. Тоді задана система
прийме вигляд:
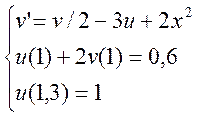
Щоб звести отриману систему до системи з крайовими умовами, виразимо v0:
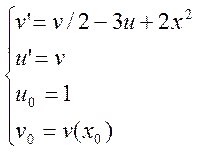
Знайдемо
v0, розклавши ![]() та
та ![]() в ряд
Тейлора:
в ряд
Тейлора:
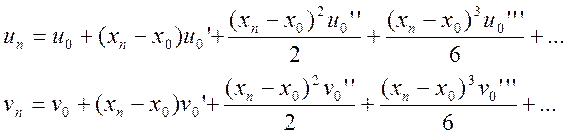
Виразимо
![]() і
і ![]() через v0 та розв’яжемо рівняння:
через v0 та розв’яжемо рівняння:
![]()
![]()
Отримаємо систему з крайовими умовами:
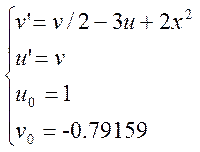
Визначимо прогноз та корекцію:
![]()
![]()
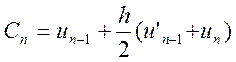
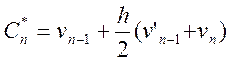
Програмна реалізація
Для реалізації програми була обрана мова програмування Delphi.
В результаті роботи програми, ми отримуємо послідовність наближень та різницю між ними, а також кінцевий результат чисельного інтегрування .
Лістинг програми
program l8;
{$APPTYPE CONSOLE}
uses SysUtils,math;
const eps=0.0001;
function vp1(v:double):double;
begin
result:=v/2-6.38;
end;
function vp2(v:double):double;
begin
result:=vp1(v)/2-3*v-5.2;
end;
function vp3(v:double):double;
begin
result:=vp2(v)/2+3*vp1(v)-4;
end;
function vp4(v:double):double;
begin
result:=vp3(v)/2+3*vp2(v);
end;
function vp5(v:double):double;
begin
result:=vp4(v)/2+3*vp3(v);
end;
function ut(u,v,h:double):double;
begin
result:=u+h*v+sqr(h)/2*vp1(v)+power(h,3)/6*vp2(v)+power(h,4)/24*vp3(v)+
power(h,5)/120*vp4(v);
end;
function vt(v,h:double):double;
begin
result:=v+h*vp1(v)+sqr(h)/2*vp2(v)+power(h,3)/6*vp3(v)+power(h,4)/24*vp4(v)
+power(h,5)/120*vp5(v);
end;
var h,v0,v1,v2,u0,u1,u2,pu,cu,pv,cv,x,z1,z2:double; i,k:word;
mas:array[0..$ffff] of double;
begin
h:=-0.1;
x:=1.3;
while true do begin
i:=1;
u1:=1;
v1:=-0.79159;
u2:=ut(u1,v1,h);
v2:=vt(v1,h);
mas[0]:=u2;
repeat begin
u0 := u1;
v0 := v1;
v1 := v2;
u1 := u2;
if x<1 then break;
x:=1.3+i*h;
z1:=v1/2-3*u1-2*sqr(x-h);
pu:= u0 + 2*h*v1;
pv:= v0 + 2*h*z1;
z2:=pv/2-3*pu-2*sqr(x);
cv:=v1+h/2*(z1+z2);
v2:=cv+(pv-cv)/5;
cu:=u1+h/2*(v1+v2);
u2:=cu+(pu-cu)/5;
mas[i]:=u2;
inc(i);
end;
until abs(pu-cu)>eps;
if not(x<1) then begin
h:=h/2;
continue;
end;
break;
end;
for k:=0 to i-2 do write(1.3+k*h:4:6,' ',mas[k]:4:6);
readln;
end.
Результат роботи програми
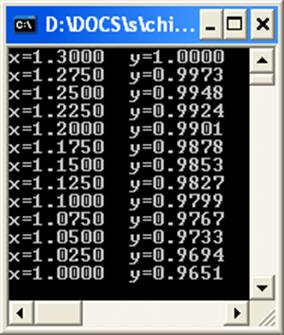
Приклад пакетної реалізації поставленої задачі
Для пакетної реалізації поставленої задачі було використано математичний пакет Maple. Результати роботи математичного пакету:
> sys1 := [diff(y(x),x,x)-diff(y(x),x)/2+3*y(x)=2*x*x,y(1.3)=1,y(1)-2*D(y)(1)=0.6];
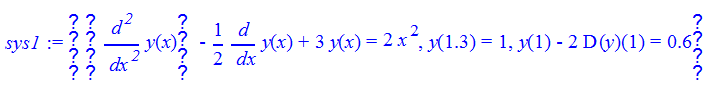
> sol1 := dsolve(sys1,numeric);
![]()
>with (plots):
> array_:=[[1.300000,1],[1.275000,0.9973],[1.250000,0.9948],[1.225000,0.9924],[1.200000,0.9901],[1.175000,0.9878],[1.150000,0.9853],[1.125000,0.9827],[1.100000,0.9799],[1.075000,0.9767],[1.050000,0.9733],[1.025000,0.9694],[1.000000,0.9651]];
![]()
![]()
![]()
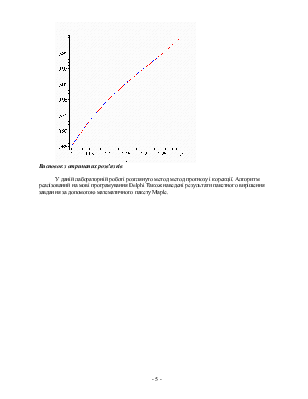
display(odeplot(sol1,color=blue),plot(array_,color=red));
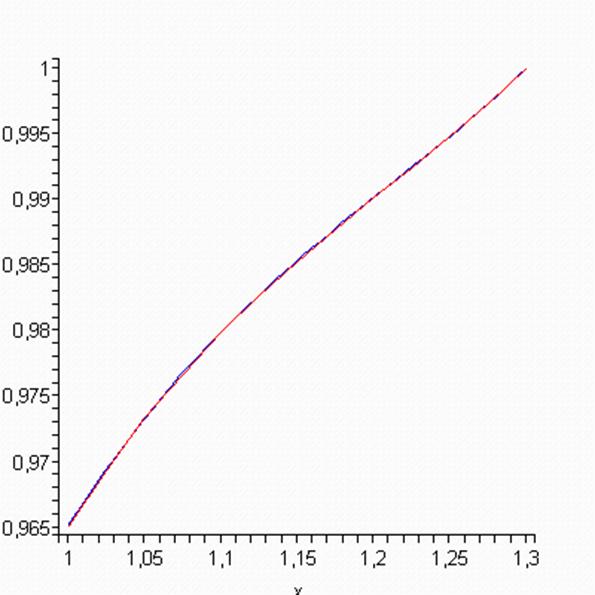
Висновок з отриманих розв’язків
У даній лабораторній роботі розглянуто метод метод прогнозу і корекції. Алгоритм реалізований на мові програмування Delphi Також наведені результати пакетного вирішення завдання за допомогою математичного пакету Maple.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.