



С целью сравнения качественных и
количественных показателей двух однотипных производственных процессов A
и B проведены выборки (x1, x2, …, xn) и (y1, y2, …, yn) объемов
nx и ny соответственно.
1. Для каждой выборки оценить математическое
ожидание a и дисперсию ![]() 2 путем: а) вычисления
выборочных средних
2 путем: а) вычисления
выборочных средних ![]() и
и ![]() ,
исправленных выборочных дисперсий
,
исправленных выборочных дисперсий ![]() и
и ![]() ; б) построения
доверительных интервалов для математических ожиданий ax и aу и дисперсий
; б) построения
доверительных интервалов для математических ожиданий ax и aу и дисперсий ![]() и
и ![]() с надежностью γ = 0,95.
с надежностью γ = 0,95.
2. Допуская, что выборки (x1, x2, … , xn) и (y1, y2, … , yn) осуществлены из нормально
распределенных генеральных совокупностей X и Y с параметрами (ax, σx) и (ay, σy) соответственно,
при уровне значимости α = 0,05: а) пользуясь критерием Фишера, проверить гипотезу ![]() =
= ![]() и установить,
является ли один из производственных процессов эффективнее другого;
б) пользуясь критерием Стьюдента, проверить гипотезу ax = aу и установить, можно ли считать распределение между средними
и установить,
является ли один из производственных процессов эффективнее другого;
б) пользуясь критерием Стьюдента, проверить гипотезу ax = aу и установить, можно ли считать распределение между средними ![]() и
и ![]() случайным,
или оно является существенным и связано с различием производственных процессов.
случайным,
или оно является существенным и связано с различием производственных процессов.
В таблице приведены показатели производительности труда рабочего, изготавливающего на станке детали до (режим работы A) и после (режим работы B) усовершенствования обработки деталей.
|
Режим работы |
Количество деталей за смену |
|||||||||
|
А |
42 |
43 |
38 |
40 |
43 |
38 |
40 |
41 |
39 |
42 |
|
В |
42 |
43 |
44 |
42 |
44 |
43 |
40 |
42 |
41 |
|
Проведем количественное и качественное сравнение производительности труда рабочего для режимов работы А и В.
Точечной оценкой математического ожидания а генеральной совокупности является выборочная
средняя. Выборочные средние ![]() и
и ![]() вычисляются по формулам:
вычисляются по формулам:
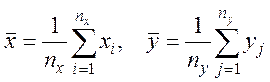 .
.
Часто удобно пользоваться формулами
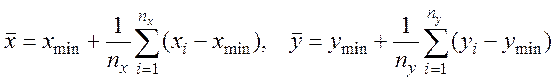 .
.
В данном случае имеем
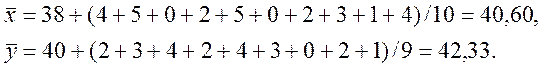
Несмещенной оценкой дисперсии σ2 генеральной совокупности является исправленная выборочная дисперсия s2. Значения ![]() и
и
![]() будем находить по формулам:
будем находить по формулам:
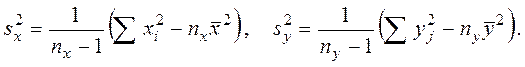
Поскольку при уменьшении всех данных выборки
на одно и то же число значение дисперсии не изменяется, то уменьшая данные
первой выборки на 38, а второй выборки
на 40, находим
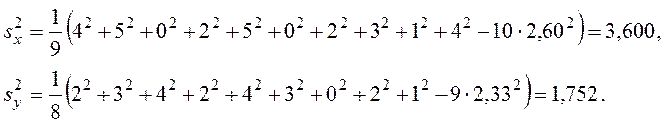 Выборочное среднее
квадратическое отклонение равно
Выборочное среднее
квадратическое отклонение равно
![]()
Для нахождения доверительного интервала математического ожидания а генеральной совокупности необходимо представить а в виде
![]()
где ![]() – точечная оценка а (среднее выборки); δ – точность оценки. Если выборка малого объема n, то точность оценки δ определяется
формулой
– точечная оценка а (среднее выборки); δ – точность оценки. Если выборка малого объема n, то точность оценки δ определяется
формулой
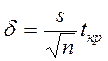 .
.
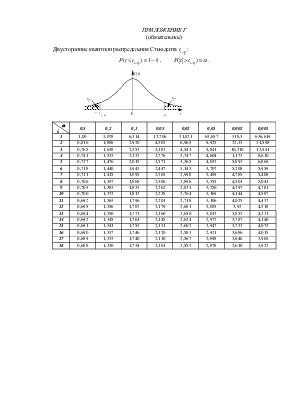
Здесь s – выборочное среднее квадратическое отклонение;
![]() – квантиль распределения Стьюдента (приложение
Г), вычисленный при уровне значимости α = 1 – γ и k = n – 1 степеней свободы.
– квантиль распределения Стьюдента (приложение
Г), вычисленный при уровне значимости α = 1 – γ и k = n – 1 степеней свободы.
Для старого режима работы А имеем:
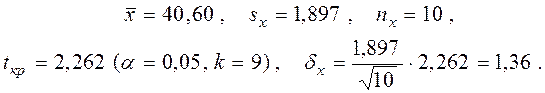
Для нового режима работы В:
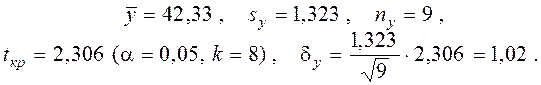
Следовательно, с надежностью γ = 0,95
![]() ,
,
т.е. доверительные интервалы для неизвестных математических ожиданий
имеют вид ![]() .
.
Это означает, что с надежностью 95% при старом режиме обработки деталей рабочий мог изготавливать 40 или 41 деталей за смену. При новом режиме обработки деталей с надежностью 95% он может изготавливать уже 42 или 43 детали за смену. Видим, что произошло качественное изменение производительности труда.
Найдем теперь доверительные интервалы для
генеральных дисперсий ![]() и
и ![]() . Для
дисперсии σ2, генеральной совокупности доверительный
интервал имеет вид
. Для
дисперсии σ2, генеральной совокупности доверительный
интервал имеет вид
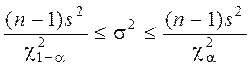 .
.
Здесь n – объем выборки; s2 – оценка
дисперсии σ2; ![]() и
и ![]() – квантили распределения Пирсона (приложение
Д), вычисленные при уровне значимости α и числе степеней
свободы k = n – 1.
– квантили распределения Пирсона (приложение
Д), вычисленные при уровне значимости α и числе степеней
свободы k = n – 1.
Для старого режима работы А:
![]()
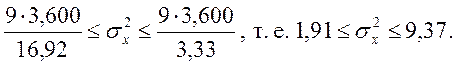
Для нового режима работы В:
![]()
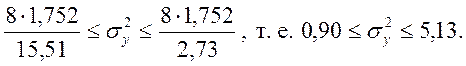
Как видим, доверительные интервалы для
генеральных дисперсий ![]() и
и ![]() пересекаются.
Поэтому с надежностью 95% у нас нет оснований отвергнуть гипотезу о равенстве
дисперсий (
пересекаются.
Поэтому с надежностью 95% у нас нет оснований отвергнуть гипотезу о равенстве
дисперсий (![]() =
= ![]() ). Это
означает, что усовершенствование обработки деталей не приводит к повышению
эффективности обработки.
). Это
означает, что усовершенствование обработки деталей не приводит к повышению
эффективности обработки.
Эффективность производственного процесса
зависит от порождаемой им дисперсии, характеризующей разброс в данных. Таким
образом, для определения эффективности нового режима работы, связанного с
усовершенствованием обработки деталей, необходимо сравнить генеральные
дисперсии ![]() и
и ![]() по данным
выборок производительности труда.
по данным
выборок производительности труда.
При сравнении двух дисперсий ![]() и
и ![]() выдвигают
нулевую гипотезу Н0:
выдвигают
нулевую гипотезу Н0: ![]() =
= ![]() ; при
конкурирующей Н1:
; при
конкурирующей Н1: ![]() ≠
≠ ![]() . Если,
по смыслу задачи, большей выборочной дисперсии (
. Если,
по смыслу задачи, большей выборочной дисперсии (![]() ) заведомо
не может соответствовать меньшая генеральная дисперсия, т.е. неравенство
) заведомо
не может соответствовать меньшая генеральная дисперсия, т.е. неравенство ![]() <
< ![]() заведомо
невозможно, то конкурирующая гипотеза приобретает вид Н1:
заведомо
невозможно, то конкурирующая гипотеза приобретает вид Н1: ![]() >
> ![]() . В этом
случае для проверки альтернативной гипотезы Н1 используется односторонний критерий Фишера
. В этом
случае для проверки альтернативной гипотезы Н1 используется односторонний критерий Фишера
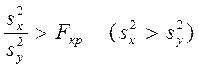 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.