Оценивание параметров и проверка статистических гипотез в случае выборок малого объема, страница 2

Здесь F_кр – критическое значение распределения Фишера (приложение Е), вычисленное при уровне значимости  и числах степеней свободы k₁ = n_x–1 и k₂ = n_y–1. Если указанное неравенство выполняется, мы склоняемся в пользу гипотезы
Н₁:  > , в противном случае, у нас нет основания отвергнуть нулевую гипотезу Н₀:  = .

В данном случае 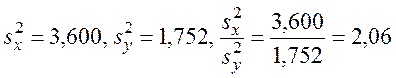. Из приложения Е при α = 0,05, k₁ = 9 и k₂ = 8 находим F_кр = 3,39. Так как 2,06 < 3,39, то мы не можем отвергнуть нулевую гипотезу и считаем равными генеральные дисперсии  и . Это означает, что усовершенствование обработки деталей, в данном случае, не является эффективным.

При сравнении двух математических ожиданий a_x и a_у выдви­гают нулевую гипотезу Н₀ : a_x = a_у, при конкурирующей гипо­тезе Н₁ : a_x ≠ a_у. Методика проверки альтернативной гипотезы Н₁ зависит от соотношения генеральных дисперсий  и .

Ранее при сравнении двух дисперсий  и  нами было установлено, что  =  = . В этом случае оценкой дисперсии σ² является средневзвешенная выборочная дисперсия

.

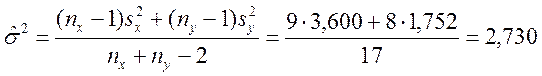Если заранее известно, что большему выборочному среднему (), не может соответствовать меньшее математическое ожидание (a_у ≥ a_x), то альтернативная гипотеза принимает вид Н₁ :  a_у > a_x. В этом случае для проверки альтернативной гипотезы Н₁ используется односторонний критерий Стьюдента

.

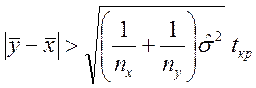Здесь t_кр – критическое значение распределения Стьюдента (приложение Г), вычисленное при уровне значимости α и числе степеней свободы k = n_x+n_y–2. Если указанное неравенство
выполняется, то гипотеза Н₁ :  a_у > a_x верна, в противном случае мы признаем справедливость нулевой гипотезы Н₀ : a_x = a_у.

В данном случае =42,33–40,60=1,73. Из приложения Г при α = 0,05 и k = 17 находим t_кр = 2,11, тогда

.

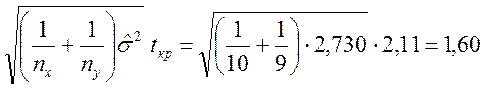Так как 1,60 < 1,73, то мы склоняемся в пользу альтернативной гипотезы Н₁ : a_у > a_x. Следовательно, расхождение между выборочными средними  и  неслучайно, при 5% уровне значимости оно является существенным и приводит к значимому повышению производительности труда после усовершенствования обработки деталей.

Отметим, что если при сравнении двух дисперсий  и  было установлено, что  >  (), то для проверки гипотезы Н₁ : a_у > a_x следует использовать односторонний критерий Стьюдента вида

,

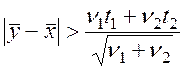где 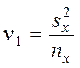; ; 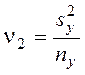t₁ и t₂ – квантили распределения Стьюдента (приложение Г), вычисленные при уровне значимости α и числах степеней свободы k₁ = n_x–1 и k₂ = n_y–1 соответственно.

ПРИЛОЖЕНИЕ Г

(обязательное)

Двусторонние квантили распределения Стьюдента :

,        .

ka	0,5	0,2	0,1	0,05	0,02	0,01	0,002	0,001
1	1,00	3,078	6,314	12,706	31,821	63,657	318,3	636,619
2	0,816	1,886	2,920	4,303	6,965	9,925	22,33	31,598
3	0,765	1,638	2,353	3,182	4,541	5,841	10,210	12,941
4	0,741	1,533	2,132	2,776	3,747	4,604	1,173	8,610
5	0,727	1,476	2,015	2,571	3,365	4,032	5,893	6,869
6	0,718	1,440	1,943	2,447	3,143	3,707	5,208	5,959
7	0,711	1,415	1,895	2,365	2,998	3,499	4,785	5,408
8	0,706	1,397	1,860	2,306	2,896	3,355	4,501	5,041
9	0,703	1,383	1,833	2,262	2,821	3,250	4,297	4,781
10	0,700	1,372	1,812	2,228	2,764	3,169	4,144	4,587
11	0,697	1,363	1,796	2,201	2,718	3,106	4,025	4,437
12	0,695	1,356	1,782	2,179	2,681	3,055	3,93	4,318
13	0,694	1,350	1,771	2,160	2,650	3,012	3,852	4,221
14	0,692	1,345	1,761	2,145	2,624	2,977	3,787	4,140
15	0,691	1,341	1,753	2,131	2,602	2,947	3,733	4,073
16	0,690	1,337	1,746	2,120	2,583	2,921	3,686	4,015
17	0,689	1,333	1,740	2,110	2,567	2,898	3,646	3,965
18	0,688	1,330	1,734	2,101	2,552	2,878	3,610	3,922