Інтелектуальні системи (модуль 5)
Практичне заняття №5
Тема: Нечітке логічне виведення
Короткі теоретичні положення
У традиційній (булевій) логіці рішення про істинність одних висловлювань приймається на основі істинності інших. Подібне виведення подається у вигляді схеми, де над горизонтальною рискою перелічуються всі висловлювання, на базі яких приймається рішення, а під ріскою – одержаний результат.
Нехай А, В та С – такі висловлювання. Подамо основні правила виведення, що застосовуються в традиційній логіці.
Модус поненс (modus ponens):
|
Умова Імплікація |
A A→B |
|
Результат |
B |
Модус толленс (modus tollens):
|
Умова Імплікація |
¬B A→B |
|
Результат |
¬A |
Сіллогізм:
|
Умова Імплікація |
A→B B→C |
|
Результат |
A→C |
Контрапозиція:
|
Умова Імплікація |
A→B |
|
Результат |
(¬B)→ (¬A) |
Модус поненс призводить до результату "B - істинно", якщо відомо, що "A - істинно" та існує правило "Якщо A, то B" (A та B - чіткі логічні умови). Але, якщо умова відсутня, то модус поненс не зможе одержати навіть наближеного результату. Навіть у випадку, коли відомо, що близьке до A висловлення A' є істинним, модус поненс не може бути застосовано. Аналогічні недоліки мають і інші правила виведення. Одним з можливих способів прийняття рішень за умов нечіткої інформації є застосування нечіткого логічного виведення
Нечітким логічним виведенням називається одержання результату у вигляді нечіткої множини, яка відповідає поточним значенням входів, з використанням нечіткої бази знань і нечітких операцій.
Основою нечіткого логічного виведення є композиційне правило Заде.
Композиційне правило виведення Задеформулюється таким чином:
Якщо відоме
нечітке відношення ![]() між вхідною
(x) і вихідною (y) змінними, то при нечіткому значені вхідної змінної
між вхідною
(x) і вихідною (y) змінними, то при нечіткому значені вхідної змінної ![]() , нечітке значення вихідної змінної
визначається як:
, нечітке значення вихідної змінної
визначається як:
![]() ,
,
де ![]() - максмінна композиція.
- максмінна композиція.
Таким чином,
![]()
де ![]() - функція належності вихідної нечіткої
множини Y,
- функція належності вихідної нечіткої
множини Y, ![]() - функція
належності вихідної нечіткої множини А,
- функція
належності вихідної нечіткої множини А, ![]() - функція
належності нечіткого відношення
- функція
належності нечіткого відношення ![]() .
.
Для формування
нечіткого відношення ![]() в композиційному
правилі Заде застосовуються такі правила:
в композиційному
правилі Заде застосовуються такі правила:
1. Правило типу мінімум
![]()
2. Правило типу добуток
![]()
3. Правила Лукашевича
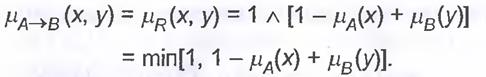
4. Правилоmax-min
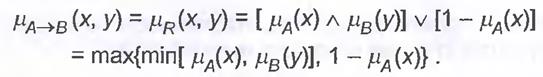
5. Бінарне правила
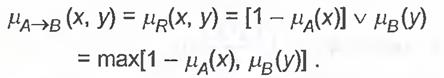
6. Правила Гогуена
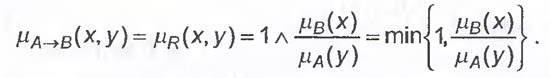
7. Правило Шарпа

8. Правило Геделя
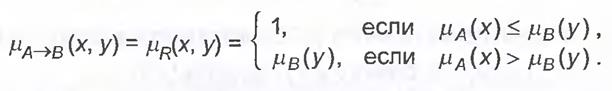
9. Імовірнісне правило
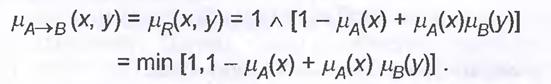
10. Правило обмеженої суми
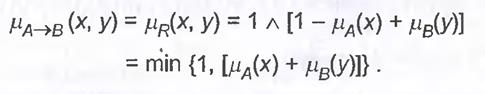
Приклад: Дано нечітке
правило "Якщо ![]() , то
, то ![]() " з нечіткими множинами:
" з нечіткими множинами: ![]() і
і ![]() . Визначити значення вихідної змінної
. Визначити значення вихідної змінної ![]() , якщо
, якщо ![]() .
.
Спочатку сформуємо нечітке
відношення, яке відповідає правилу "Якщо ![]() , то
, то ![]() ", застосовуючи правило типу мінімум:
", застосовуючи правило типу мінімум:
 .
.
Тепер, по формулі ![]() обчислимо нечітке значення вихідної
змінної:
обчислимо нечітке значення вихідної
змінної:
![]() .
.
Практичні завдання
Дано нечітке
правило "Якщо ![]() , то
, то ![]() ". Визначити значення вихідної
змінної
". Визначити значення вихідної
змінної ![]() , якщо
, якщо ![]() . Для формування
нечіткого відношення
. Для формування
нечіткого відношення ![]() в композиційному
правилі Заде застосувати не менш ніж три різні правила, одне з яких повинно
бути правилом типу мінімум. Програмну реалізацію виконати за допомогою пакетів
MatLab та Excel.
в композиційному
правилі Заде застосувати не менш ніж три різні правила, одне з яких повинно
бути правилом типу мінімум. Програмну реалізацію виконати за допомогою пакетів
MatLab та Excel.
|
Варіант 1 A = (0.3/a, 0.9/b, 0.8/c, 0.4/d, 0.3/e), B = (0.3/X, 0.9/Y, 0.8/Z, 0.3/V ), C = (0.3/a, 0.2/b, 0.4/c, 0.5/d, 0.1/e). |
Варіант 11 A = (0.3/a, 0.3/b, 0.4/c, 0.7/d, 0.5/e), B = (0.3/X, 0.3/Y, 0.4/Z, 0.5/V ), C = (0.4/a, 0/b, 0.8/c, 0.6/d, 0.2/e). |
|
Варіант 2 A = (1/a, 0.2/b, 0.2/c, 0.7/d, 0.1/e), B = (1/X, 0.2/Y, 0.2/Z, 0.1/V ), C = (0.5/a, 0.2/b, 0.7/c, 0.2/d, 0.5/e). |
Варіант 12 A = (0.7/a, 0.5/b, 0.2/c, 0.6/d, 0.9/e), B = (0.7/X, 0.5/Y, 0.2/Z, 0.9/V ), C = (0.6/a, 0.6/b, 0.9/c, 0.3/d, 0.4/e). |
|
Варіант 3 A = (0.3/a, 0.8/b, 0.9/c, 1/d, 0.5/e), B = (0.3/X, 0.8/Y, 0.9/Z, 0.5/V ), C = (0.4/a, 0/b, 0.8/c, 0.2/d, 1/e). |
Варіант 13 A = (0.4/a, 1/b, 0.2/c, 0.9/d, 0.5/e), B = (0.4/X, 1/Y, 0.2/Z, 0.5/V ), C = (0.7/a, 0.2/b, 0.6/c, 0.7/d, 0.3/e). |
|
Варіант 4 A = (1/a, 0.6/b, 1/c, 0.1/d, 0.5/e), B = (1/X, 0.6/Y, 1/Z, 0.5/V ), C = (0.9/a, 0.3/b, 0.2/c, 0.3/d, 0.3/e). |
Варіант 14 A = (0.7/a, 0.6/b, 0.5/c, 0.6/d, 0.1/e), B = (0.7/X, 0.6/Y, 0.5/Z, 0.1/V ), C = (0.7/a, 0.3/b, 0/c, 0.5/d, 0.7/e). |
|
Варіант 5 A = (0.2/a, 0.1/b, 0.8/c, 0.6/d, 0.1/e), B = (0.2/X, 0.1/Y, 0.8/Z, 0.1/V ), C = (0.2/a, 0.5/b, 0.3/c, 0.5/d, 0.7/e). |
Варіант 15 A = (0.8/a, 0.9/b, 0.3/c, 0.5/d, 0.8/e), B = (0.8/X, 0.9/Y, 0.3/Z, 0.8/V ), C = (0.7/a, 0.9/b, 0.4/c, 1/d, 0.4/e). |
|
Варіант 6 A = (0.9/a, 0/b, 0.2/c, 0.6/d, 0.5/e), B = (0.9/X, 0/Y, 0.2/Z, 0.5/V ), C = (0.3/a, 0.7/b, 0.6/c, 0.5/d, 0.7/e). |
Варіант 16 A = (0.1/a, 0.6/b, 0.1/c, 0.1/d, 0.8/e), B = (0.1/X, 0.6/Y, 0.1/Z, 0.8/V ), C = (0.2/a, 0.5/b, 0.5/c, 0.9/d, 0.4/e). |
|
Варіант 7 A = (0/a, 0.2/b, 0.4/c, 0.1/d, 1/e), B = (0/X, 0.2/Y, 0.4/Z, 1/V ), C = (0.5/a, 0.6/b, 0.6/c, 0.9/d, 0.3/e). |
Варіант 17 A = (0.9/a, 0.7/b, 0.1/c, 0.1/d, 0.9/e), B = (0.9/X, 0.7/Y, 0.1/Z, 0.9/V ), C = (0.6/a, 0.5/b, 0.8/c, 0.6/d, 0.9/e). |
|
Варіант 8 A = (0.7/a, 0.2/b, 0.1/c, 0.9/d, 0.6/e), B = (0.7/X, 0.2/Y, 0.1/Z, 0.6/V ), C = (0.5/a, 0.2/b, 0.8/c, 0.1/d, 0/e). |
Варіант 18 A = (0.9/a, 0.1/b, 0.1/c, 0.5/d, 0.1/e), B = (0.9/X, 0.1/Y, 0.1/Z, 0.1/V ), C = (0.7/a, 0.5/b, 0.8/c, 0.6/d, 0.6/e). |
|
Варіант 9 A = (1/a, 1/b, 0.6/c, 0.5/d, 0/e), B = (1/X, 1/Y, 0.6/Z, 0/V ), C = (0.5/a, 0.3/b, 0.7/c, 0.5/d, 0.8/e). |
Варіант 19 A = (0.1/a, 0.2/b, 0.7/c, 0.3/d, 0.6/e), B = (0.1/X, 0.2/Y, 0.7/Z, 0.6/V ), C = (0.8/a, 0.6/b, 0.7/c, 0/d, 0.6/e). |
|
Варіант 10 A = (0.6/a, 0.4/b, 0.5/c, 0.9/d, 0.1/e), B = (0.6/X, 0.4/Y, 0.5/Z, 0.1/V ), C = (0.6/a, 0.8/b, 0.1/c, 0.7/d, 0/e). |
Варіант 20 A = (0.1/a, 1/b, 0.8/c, 0.1/d, 1/e), B = (0.1/X, 1/Y, 0.8/Z, 1/V ), C = (0.6/a, 0.7/b, 0.3/c, 0.9/d, 0.7/e). |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.