правила
ПРИКЛАДИ ВИКОНАННЯ КОНТРОЛЬНИХ ЗАВДАНЬ
ПРИКЛАД 1 - Розв’язання завдання на тему «Одношаровий персептрон»
Модель персептрона має такий вигляд (рис. 1):
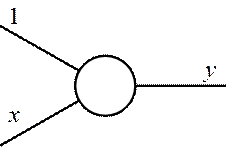
Рис. 1. – Модель персепртрона
При цьому
x ![]() Rd, або
x
Rd, або
x ![]() {–1, 1}d,
{–1, 1}d,
y ![]() R, або y
R, або y ![]() {–1, 1}.
{–1, 1}.
Таку модель використовують для розв’язання задачі класифікації для двох класів і є ідентичною до задачі
y ![]() {0, 1}.
{0, 1}.
Будемо розглядати випадок
x ![]() Rd, y
Rd, y
![]() {–1, 1}.
{–1, 1}.
Функціонування персептрона описується наступною залежністю:
y = sign(WTx – τ) = f(x, W). (1)
де τ – деякий поріг, W – вектор вагових коефіцієнтів персептрона.
У геометричній інтерпретації рівняння (1) визначає два підпростори
{x : y = 1} ![]() H+ = {x : WTx
H+ = {x : WTx
![]() τ },
τ },
{x : y = –1} ![]() H– = {x : WTx
< τ }, (2)
H– = {x : WTx
< τ }, (2)
з роздільною гіперплощиною (афінний підпростір розмірності d – 1):
H = {x : WTx – τ = 0}.(3)
Збільшуючи розмірність простору, отримаємо
x
![]() Rd
Rd ![]()
![]()
![]() Rd+1, (4)
Rd+1, (4)
де ![]() =
= ![]() ,
, ![]() = 1, і
= 1, і
![]() d,
d,
W
![]() Rd
Rd ![]()
![]()
![]() Rd+1, (5)
Rd+1, (5)
де ![]() =
= ![]() ,
, ![]() = τ,
і
= τ,
і ![]() d.
d.
Враховуючи (4) та (5), можна записати
WTx – τ = ![]() T
T![]() .
.
Навчання персептрона (алгоритм Розенблатта)
Навчання персептрона представляє собою процес налаштування вагових коефіцієнтів W. При навчанні нейронної мережі, як правило, математичні вирази для розділяючих поверхонь відсутні. Тому навчання виконується тільки на навчальній вибірці.
Навчальна вибірка (скінчена) задається множиною, що складається з пар вхід-вихід:
T = {(x1, t1), …, (xn, tn)} = {(xi, ti), i = 1, …, n},(6)
де ![]() {–1, 1}.
{–1, 1}.
Мета навчання – налаштувати вагові коефіцієнти
W таким чином, щоб для будь-яких виконувалось x* ![]() Rd, x*
Rd, x* ![]() T виконувалось y = t*.
T виконувалось y = t*.
Алгоритм навчання персептрона Розенблатта:
Даний алгоритм коректно працює лише в тих випадках, коли класи є лінійно роздільними.
1. Формуємо множину
2.
![]() ,
,
де
![]() ={x: якщо існує і
таке, що
={x: якщо існує і
таке, що ![]() = 1, х = хі},
= 1, х = хі},
![]() ={x: якщо існує і
таке, що
={x: якщо існує і
таке, що ![]() = –1, х = хі}
= –1, х = хі}
![]() ={
={![]() :
:![]() ,
, ![]() },
},
і систему
![]() T
T![]() >0 для будь яких
>0 для будь яких ![]() .
.
3.
Початок. Вибираємо деякий
елемент ![]() як початкове наближення для
як початкове наближення для![]() . Сформуємо випадкову послідовність
(циклічну, у якій елементи з'являються з невизначеною частотою) з елементів
. Сформуємо випадкову послідовність
(циклічну, у якій елементи з'являються з невизначеною частотою) з елементів ![]() .
.
4.
Тест. Вибираємо випадкове
значення ![]() = rand(
= rand(![]() ). Якщо
). Якщо ![]() T
T![]() > 0
, переходимо до п. 3, інакше –– до п. 4.
> 0
, переходимо до п. 3, інакше –– до п. 4.
5. Модифікація вагових коефіцієнтів.
![]() ,
,
де ![]() = 1.
= 1.
Переходимо до п. 3.
6.
Завершення. Процес
навчання закінчується тоді, коли умова ![]() T
T![]() > 0 буде виконуватися для
всіх векторів навчальної вибірки.
> 0 буде виконуватися для
всіх векторів навчальної вибірки.
Розрахунки
|
c |
|
|
Варіант № 2 |
||||||||||
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|||
|
x1 |
10 |
10 |
10 |
11 |
9 |
10 |
11 |
9 |
11 |
9 |
|||
|
x2 |
18 |
16 |
15 |
14 |
12 |
9 |
11 |
10 |
10 |
10 |
|||
|
Збільшуємо розмірність простору, |
Рис. 2 – Графічне подання лінійного вирішального правила |
||||||||||||
|
x3 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||
|
Вказуємо значення параметру t = y |
|||||||||||||
|
t |
1 |
1 |
1 |
1 |
1 |
-1 |
-1 |
-1 |
-1 |
-1 |
|||
|
Формуємо матрицю |
|||||||||||||
|
z1 |
10 |
10 |
10 |
11 |
9 |
-10 |
-11 |
-9 |
-11 |
-9 |
|||
|
z2 |
18 |
16 |
15 |
14 |
12 |
-9 |
-11 |
-10 |
-10 |
-10 |
|||
|
z3 |
1 |
1 |
1 |
1 |
1 |
-1 |
-1 |
-1 |
-1 |
-1 |
|||
|
Вибираємо деякий елемент Перевіряємо виконання умови |
|||||||||||||
|
|
10 |
|
425 |
389 |
371 |
363 |
307 |
-263 |
-309 |
-271 |
-291 |
-271 |
|
|
18 |
|||||||||||||
|
1 |
|||||||||||||
|
Проводимо модифікацію вагових коефіцієнтів |
|||||||||||||
|
|
0 |
|
162 |
144 |
135 |
126 |
108 |
-81 |
-99 |
-90 |
-90 |
-90 |
|
|
9 |
|||||||||||||
|
0 |
|||||||||||||
|
Проводимо модифікацію вагових коефіцієнтів де |
|||||||||||||
|
|
-10 |
|
-101 |
-101 |
-101 |
-111 |
-91 |
101 |
111 |
91 |
111 |
91 |
|
|
0 |
|||||||||||||
|
-1 |
|||||||||||||
|
Проводимо модифікацію вагових коефіцієнтів |
|||||||||||||
|
|
0 |
|
324 |
288 |
270 |
252 |
216 |
-162 |
-198 |
-180 |
-180 |
-180 |
|
|
18 |
|||||||||||||
|
0 |
|||||||||||||
|
Проводимо модифікацію вагових коефіцієнтів |
|||||||||||||
|
|
-10 |
|
61 |
43 |
34 |
15 |
17 |
20 |
12 |
1 |
21 |
1 |
|
|
9 |
|||||||||||||
|
-1 |
|||||||||||||
|
Таким
чином, лінійне вирішальне правило y = sing(–10x1 +9 x2 –1). Графічний вигляд сформованого правила подано на рис.2. |
|||||||||||||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.