Контекстовільні мови. Дерева розбору. Неоднозначні граматики

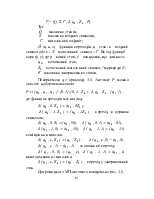
3 КОНТЕКСТОВІЛЬНІ МОВИ

3.1 Дерева розбору

Домовимося далі для позначення терміналів використовувати малі букви з початку алфавіту (такі, як  a, b, c), символи, цифри,  рядки, виділені жирним шрифтом (такі, як  id, if). Нетермінали будемо позначати великими буквами з початку алфавіту (A, B, C), рядками, виділеними курсивом (stmt, expr). Великі букви з кінця алфавіту (X, Y, Z) будуть позначати граматичні символи, тобто або термінали, або  нетермінали. Малі букви з кінця алфавіту (u, v, ... , z) – рядки терміналів. Малі грецькі букви (такі, як  α, β, γ) будуть представляти рядки граматичних символів.

Візьмемо  граматику для побудови виразів типової мови програмування. Обмежимося операторами  “+”, “*”,  а як аргументи візьмемо ідентифікатори, що починаються символами а або b, а далі йде ланцюжок з  а,b,0,1.

 Граматика може мати вигляд G=({E,I}, T, P, E), де

T={+, *,  (,  ),  a,  b, 0, 1},  а P – множина продукцій:

E  →  I , I   →   B,

 E  → E + E , I   →   Ia,

 E  →  E * E,  I   →  Ib, 

 E  →   (E),         I   →  I0,

 I   →    a,              I   →  I1.

Надалі нетермінали будемо називати також змінними.

Для обмеження числа виборів у процесі породження будемо заміняти крайню ліворуч змінну тілом її продукції.

             E    E * E    I * E     a * E    a * (E) 

 a *(E + E)    a * (I + E)    a * (a + E)

  a * (a + I)      a* (a + I0)     a * (a + b0) .

Таке породження будемо називати лівим і позначати через , від слова leftmost (зліва).

Аналогічно будуються праві породження, що позначаються через , від слова rightmost (справа).

  E       E * E      E *(E)     E *(E + E) 

    E * (E + I)       E * (E + I0)     E *(E + b0) 

   E * (I + b0)        E *(a + b0)       a * (a + b0).

Будь-яке породження має еквівалентні ліве і праве породження.

Приклад виконання завдання.Є граматика з продукціями

 S  →  if E then S else S | if E then S | other .

Показати, що ланцюжок

            if E then if E then other elseother

має два лівих породження.

            Перше породження має вигляд:

S  if E then S else S  if E then if E then S else S

 if E then if E then otherelse S

 if E then if E then otherelseother.

Друге породження має вигляд:

S  if E then S  if E then if E then S else S

 if E then if E thenotherelse S

 if E then if E thenotherelseother.

Наступним важливим поняттям є дерева розбору.

Будемо розглядати граматику

                            G= (V, T, P, S).

Дерева розбору    для G – це  дерева з такими властивостями.

1  Кожен внутрішній вузол позначений змінною з множини V.

2  Кожен лист позначений змінною або терміналом, або ε.

3   Якщо дочірні вузли вузла A позначені зліва направо   X₁, X₂, … , X_k ,   то  A →  X₁X₂… X_k  є  продукцією в P.

Якщо подивитися на листи дерева розбору і виписати їх позначення зліва направо, одержимо ланцюжок, що називається кроною дерева і завжди є ланцюжком, виведеним зі змінної, яка позначає корінь.

Особливий інтерес становить дерево, корінь якого відмічений стартовим символом, а крона є термінальним ланцюжком.

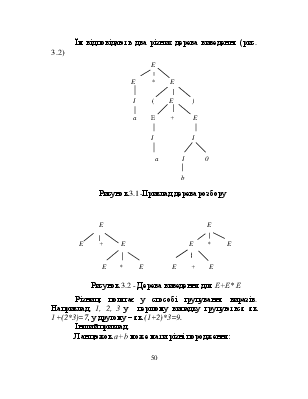
Дерево розбору для попереднього прикладу зображене  на рис. 3.1.

3.2 Неоднозначні граматики

Граматики можуть бути неоднозначними.

Повернемося до граматики виразів. Ланцюжок  Е+Е* Е має два породження:

1)    Е      Е  + Е      Е + Е * Е ;

            2)    Е      Е  * Е      Е + Е * Е.

Їм відповідають два різних дерева виведення (рис. 3.2)

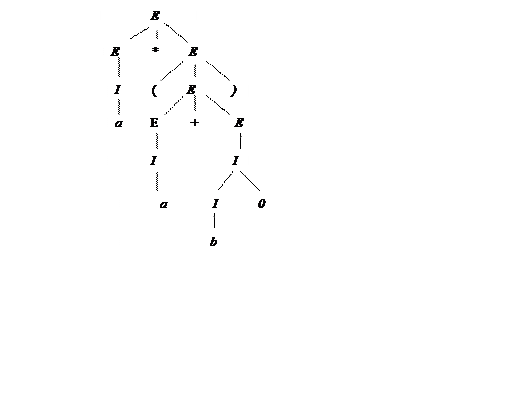                   Рисунок 3.1-Приклад дерева розбору

Рисунок 3.2 - Дерева виведення для Е+Е* Е

Різниця полягає у способі групування виразів. Наприклад, 1, 2, 3 у  першому випадку групуються як 1+(2*3)=7, у другому – як (1+2)*3=9.

Інший приклад.

Ланцюжок а+b може мати різні породження:

E  E + E   I + E    a + E    a + I   a + b       і

E   E + E   E + I  I + I    I + b    a + b .

Обидва породження приводять до одного дерева розбору.

Таким чином, неоднозначність походить не від наявності багатьох породжень, а від існування двох і більше дерев розбору.

Є дві причини неоднозначності:

- не враховується пріоритет операторів;

- не враховується асоціативність операторів.

Рішенням проблеми неоднозначності може бути введення декількох змінних з різними можливостями зв'язування. Для прикладу можна ввести такі змінні.

Співмножник  (factor) F, який не може бути розірваний на частини за допомогою “*”  і “+”, які примикають зліва або справа.

Доданок (term) T , який не може бути розірваний оператором “+”. Наприклад, a*b не може бути розірваний оператором “+”, але може бути розірваний оператором “*”: a1*a*b=(a1*a)*b.

Вираз (expression) E – будь-який вираз, включаючи ті, які можуть бути розірвані  за допомогою “* ”  і “ + ”.