Контекстовільні мови. Дерева розбору. Неоднозначні граматики, страница 4

            A → αА',

            А' → β₁ | β₂ .

            Алгоритм 3.2  Ліва факторизація граматики

            Для кожного  нетермінала A шукаємо найдовший префікс α, спільний для двох  або більше його альтернатив. Якщо α ≠ ε, тобто існує нетривіальний спільний  префікс, заміняємо  всі A-продукції A → αβ₁ | αβ ₂ | ... | αβ _n | γ, де γ представляє  всі альтернативи, які не починаються з α, продукціями:

            A → αА' | γ ,

            А' → β₁ | β₂ | ... | β_n .

            Тут А' – новий нетермінал.  Повторно   застосовуємо   це перетворення, поки  ніякі дві  альтернативи не будуть мати спільний префікс.

            Розглянемо знову граматику умовних операторів:

            S →  iEtS | iEtSeS| a ,

            E→b .

Тут  i, t, e означають if, then, else, E і S відповідають expr і stmt.

            Після лівої факторизації граматика набере такого вигляду:

            S →  iEtSS' | a ,

S'→ eS | ε,

            E→ b .

3.5Магазинні автомати

Магазинний автомат – це власне кажучи ε-НСА  з  додаванням магазина

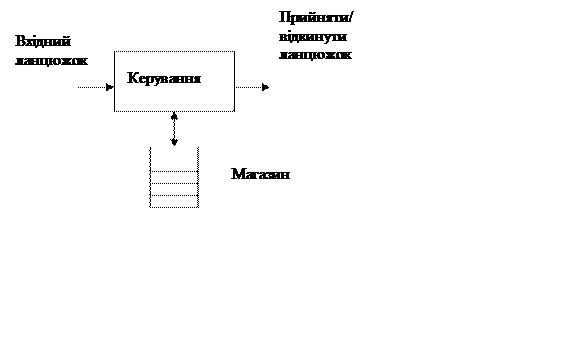
Рисунок 3.5 - Схема магазинного автомата

Магазин може читатися, до його вершини можуть додаватися символи, і вони ж можуть зніматися з вершини.            Магазинний автомат може робити перехід на основі поточного стану, вхідного символа і символа на вершині магазина.

За один перехід автомат робить дії:

- читає і пропускає символ вхідного ланцюжка (якщо ε - символ не пропускається);

- переходить у новий стан, який може і не відрізнятися від поточного;

- заміняє символ на вершині магазина деяким ланцюжком.

Варіанти роботи магазина. 

-  Ланцюжок дорівнює ε, це відповідає зняттю з вершини магазина.

- Ланцюжок дорівнює символові, що був на вершині. Магазин не змінюється.

- Ланцюжок дорівнює довільному символові. Замінюється символ на вершині магазина.

- Ланцюжок дорівнює декільком символам, це відповідає поміщенню в магазин декількох символів.

Приклад 3.1  Мова, утворена паліндромами парної довжини з  0  і  1,

        L = {w w^R  |  w ( 0 | 1)},

де w^R  позначає обернений ланцюжок.

  Стан  q відповідає припущенню, що не досягнута середина слова. Символи читаються, а їх копії записуються в магазин.

 Припущення про те, що досягнуто середину слова, викликає спонтанний перехід у q .  У цьому стані вхідні символи порівнюються із символами на вершині магазина. При збігу магазинний символ віддаляється.

При спустошенні магазина виконується перехід у завершальний стан q .

Формальне визначення МП – автомата.

Запис містить 7 компонентів:

        P = (Q, Σ, Г, δ, q , Z , F).

Тут

 Q    – множина станів;

 Σ    – множина вхідних символів;

  Г   – магазинний алфавіт;         

(q, a, x) – функція переходів: q – стан; а – вхідний символ або ε ; Х – магазинний символ з Г. Вихід функції – пари (p, γ), де p – новий стан; γ – ланцюжок, що заміняє x;

q – початковий стан;

Z – початковий магазинний символ, “маркер дна”;     

F – множина завершальних станів.

Повернемося до прикладу 3.1. Автомат P можна описати набором компонент

P =( {q , q , q }, {0, 1},{ 0, 1,  Z }, δ, q , Z , { q } ),

де функція переходів має вигляд:

δ ( q , 0, Z ) = (q , 0Z );

 δ ( q , 1, Z ) = (q , 1Z ) –  перехід за першим символом;

δ ( q , 0, 0) = (q , 00),     δ ( q , 0, 1) = (q , 01),

δ ( q , 1, 0) = (q , 10),   δ ( q , 1, 1) = (q , 11)  –  поміщення в магазин;

δ ( q , ε, Z ) = (q , Z ),       δ ( q , ε ,0) = (q ,0),