Контекстовільні мови. Дерева розбору. Неоднозначні граматики, страница 5

δ ( q , ε , 1) = (q , 1)  – спонтанний перехід;

δ ( q , 0, 0) = (q , ε),  δ ( q , 1, 1) = (q , ε) – виштовхування з магазина;

δ ( q , ε, Z ) = (q , Z ) – перехід у завершальний стан.

Діаграма цього МП-автомата наведена на рис. 3.6.

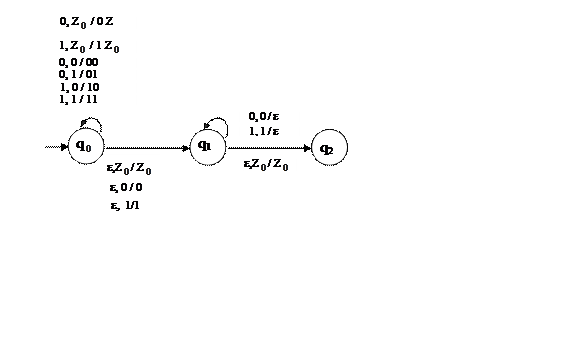
Рисунок 3.6 - Діаграма переходів МП-автомата з прикладу 3.1

Наведемо приклад його роботи на ланцюжку 1111 (рис. 3.7).

Ми розглядали  МП-автомати, що завершували роботу мовою L по  досягненні  завершального  стану.  Можна побудувати автомат, що завершує роботу при спустошенні магазина.

Якщо для деякої мови існує МП-автомат, що закінчує    роботу   по  досягненні  завершального  стану,    то існує і МП-автомат автомат для цієї мови, що завершує роботу при спустошенні магазина.

Справедливо і зворотне.

Клас контекстовільних мов  відповідає класові мов, що допускаються МП-автоматами.

Становлять інтерес детерміновані МП-автомати (ДМП-автомати).

МП-автомат є детермінованим, якщо функція переходів має тільки одну пару значень для кожної трійки аргументів (при цьому, якщо значення δ (q, a, X) не порожнє,  значення δ (q, ε , X) повинне бути порожнім).

 

Рисунок 3.7 - Робота МП-автомата на ланцюжку 1111

Якщо  мова регулярна, вона є припустимою для деякого ДМП-автомата.

Мови ДМП-автоматів містять у собі всі регулярні мови (рис. 3.7).

Рисунок 3.8 - Співвідношення регулярних мов,

 ДМП-мов  і  КВ-мов

Класи  мов, що допускаються ДМП-автоматами по  досягненні  завершального  стану і при спустошенні магазина, не збігаються.

Мови ДМП-автоматів мають однозначну граматику.

У той самий час існують мови з однозначною граматикою, що не є  ДМП-мовами.

Наведемо деякі властивості контекстовільних мов.

Теорема (без доведення). Кожна контекстовільна мова породжується граматикою, усі продукції якої мають форму А → ВР або А → а, де А, В, P – змінні; а – термінал. 

Ця форма називається нормальною формою Хомського.

Лема  про розширення для контекстно-вільних мов. Нехай L – контекстовільна мова. Тоді існує така константа n, що якщо z – довільний ланцюжок довжини не менше n, то її можна подати у вигляді z = uvwxy, де

1)   | vwx |  ≤ n;

2)   vx ≠ ε;

3)   uvⁱwxⁱy  L для всіх   і ≥ 0.

Лема про розширення  часто використовується при доведенні того, що мова не є контекстовільною.

Контекстовільні мови замкнені щодо операцій об'єднання, конкатенації, замикання і суперпозиції.

Завдання до розділу 3

1  Написати граматику,   яка для алфавіту {0,1} генерує всі рядки, включаючи порожній.

2    Є граматика з продукціями

PROGRAM  →  begin DECS ; STATS end

DECS → D ; DECS  | D

STATS    →  S ; STATS | S  .

Написати ліве породження для

            begin D ; D ; S ; S end

3 Побудувати контекстовільну граматику, що генерує множину ланцюжків { 0ⁿ1ⁿ  | n ≥ 1}.

4 Подана граматика породжує мову регулярного вирзу { 0*1(0|1)* }:

S → A1B ,  A → 0A | ε ,   B → 0B | 1B | ε.

Записати ліве  породження для ланцюжка 00101.

5 Подана граматика породжує мову регулярного виразу {0*1(0|1)* }:

S → A1B ,  A → 0A | ε ,   B → 0B | 1B | ε.

Записати праве породження для ланцюжка 1001.

6 Подана граматика породжує мову регулярного виразу {0*1(0|1)* }:

S → A1B ,  A → 0A | ε ,   B → 0B | 1B | ε.

Записати ліве і праве породження для ланцюжка 00011.

7 Подана граматика породжує мову регулярного виразу {0*1(0|1)* }:

S → A1B ,  A → 0A| ε ,   B → 0B|1B| ε.

Записати ліве і праве породження для ланцюжка 00010.