Контекстовільні мови. Дерева розбору. Неоднозначні граматики, страница 2

Мову, задану попередньою граматикою, можна за допомогою введених нами змінних E,T і F задати ще однією граматикою, яка є однозначною.

            E  T | E + T,

T  F | T * F,

F I | (E) ,

I a | b | Ia | Ib | I0 | I1 .

Дана граматика враховує як лівоасоціативність, так і пріоритет операторів.

            Розглянемо ще один приклад граматики для побудови умовного оператора.

            stmt → if expr then stmt

                        | if expr then stmt else stmt

                        | other .

            Ця граматика є неоднозначною, оскільки рядок

            if expr1 then if expr2 then stmt1 else stmt2

 має два дерева розбору (рис. 3.3).

Рисунок 3.3 - Два дерева розбору для  stmt

В усіх мовах програмування з умовними інструкціями такого виду перевага віддається першому дереву розбору. Загальне правило  говорить “зіставити кожне else найближчому ліворуч незайнятому then”. Це правило усунення неоднозначності може бути вбудоване безпосередньо в граматику. Основна ідея полягає у тому, що інструкція, що з'являється між then і else, повинна бути збалансованою (matched): вона може бути або повною інструкцією if-then-else, або інструкцією, що відрізняється від умовної.

Виходячи з цього, побудуємо граматику:

stmt → matched_stmt

| unmatched_ stmt ,

matched_stmt → if expr then matched_stmt else matched_stmt

| other ,

unmatched_stmt→ if expr then stmt

| if expr then matched_stmt else unmatched_stmt .

Ця  граматика генерує ту саму множину рядків, але дає тільки одне дерево розбору, яке зіставляє кожне else найближчому ліворуч незайнятому then.

 Якщо хоча б одна граматика мови L однозначна, то L є однозначною мовою.

            Мова виразів, породжувана попередніми граматиками, є однозначною.

Хоча породження не завжди унікальні, навіть якщо граматика однозначна, виявляється, що в однозначній граматиці і ліві, і праві породження унікальні.

Тому для дослідження неоднозначності можна брати, наприклад, тільки ліві породження.

Контекстовільна мова називається істотно неоднозначною, якщо всі її граматики неоднозначні.

Наведемо приклад істотно неоднозначної мови.

L = {aⁿ bⁿ c^m d^m | n,m≥1}  {aⁿ b^m c^m dⁿ | n,m≥1} ;

S  AB  | C,

A  aAb  | ab ,

B  cBd  | cd ,

C  aCd  | aDd ,

B bDc  | bc .

Усі ланцюжки цієї мови породжуються двома різними шляхами. Наприклад, для ланцюжка aabbccdd будуть отримані дерева розбору, зображені на рис. 3.4.

У даному прикладі всі ланцюжки породжуються двома різними шляхами.

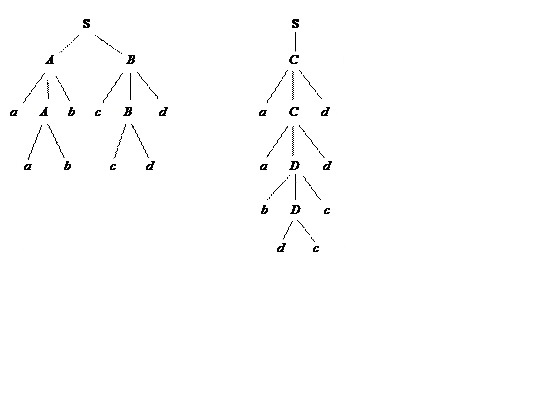
Рисунок 3.4 - Дерева розбору для  істотно неоднозначної мови

Для того щоб переконатися, що ланцюжок належить деякій мові, є два  види аналізу.

Перший вид – спадний аналіз, або аналіз “зверху-вниз”, коли стартовий символ послідовно розгортається в ланцюжок. Популярність аналізаторів “зверху-вниз” обумовлена тим фактом, що побудувати ефективний аналізатор вручну простіше з використанням методу “зверху-вниз”.

Другий вид – висхідний аналіз, або аналіз “знизу- вгору”, коли ланцюжок послідовно згортається до стартового символа.

Позначимо корінь дерева через A. Наступні твердження рівносильні.

            1  Згортка переводить ланцюжок w у A .

            2   A     w .

            3   A     w .

            4   A     w .

              5  Існує дерево розбору з коренем А і кроною w.

3.3 Видалення лівої рекурсії

            Граматика ліворекурсивна,  якщо в  ній є нетермінал  A такий, що  існує породження  A Aα для  деякого рядка  α. Ліворекурсивні граматики  не можуть  аналізуватися методами “зверху-вниз”, тому необхідне видалення лівої рекурсії.