Методології програмування. Основні методології

6 МЕТОДОЛОГІЇ ПРОГРАМУВАННЯ

6.1Основні методології

Методологія – це сукупність методів, об'єднаних загальним філософським підходом.

Коли говорять про методології на стадії розроблення програми, часто використовують термін  “парадигма програмування”.

Парадигма програмування  – це зведення теоретичних основ і правил програмування, не зв'язане з конкретною мовою.

Розрізняють такі типи програмування залежно від методології:

-   імперативне;

-   об’єктно-орієнтоване;

-   функціональне;

-   логічне.

6.2Імперативне програмування

Імперативне програмування ґрунтується на описі послідовної зміни станів обчислювача. Якщо під обчислювачем розуміти сучасний комп'ютер, то його станом будуть значення всіх комірок пам'яті, стан процесора і зв'язаних з ним пристроїв. Цей тип програмування орієнтований на класичну модель фон Неймана.

Імперативне програмування як модель використовує машину Тьюринга.

Основна синтаксична одиниця – оператор. Розрізняють атомарні і структурні оператори. Для опису синтаксису часто використовують систему позначень Бекуса-Наура.

Імперативні мови  –  Pascal, C та інші.

Сфера застосування – керування апаратними засобами і розв’язання невеликих задач.

Розвитком імперативного програмування є структурне програмування, що полягає у покроковій деталізації програми і використанні тільки трьох керуючих конструкцій: чергування, умови і циклу.

6.3Об’єктно-орієнтоване програмування

При об'єктному підході досліджувану систему представляють у вигляді об'єктів і зв'язків між ними, а поводження системи визначається змістом повідомлень між об'єктами.

Мови об'єктного програмування можна поділити на:

              -   чисті: Simula, Smalltalk;

              - гібридні, які з'явилися внаслідок впровадження в імперативні мови об'єктних конструкцій: C++, Object Pascal;

               -  урізані, які з'явилися внаслідок видалення з гібридних мов найбільш небезпечних конструкцій: Java, C#.

Об'єктна мова повинна підтримувати інкапсуляцію, спадкування і поліморфізм.

Інкапсуляція – це приховання даних і комбінування даних і методів в одному об'єкті.

Спадкування – одержання даних і методів похідними класами від базових. По суті, спадкування дозволяє повторно використовувати існуючі визначення класів.

Якщо клас не має у своєму розпорядженні методу для обробки повідомлення, повідомлення може бути передане вгору, по ієрархії класів.

Якщо оброблювач події вибирається на етапі виконання програми, метод називається віртуальним.

Поліморфізм – розходження в дії методів, які мають однакові імена, але знаходяться в різних місцях ієрархії. Поліморфізм дозволяє приховувати різні реалізації за однаковим інтерфейсом.

              Поліморфізм має різновиди

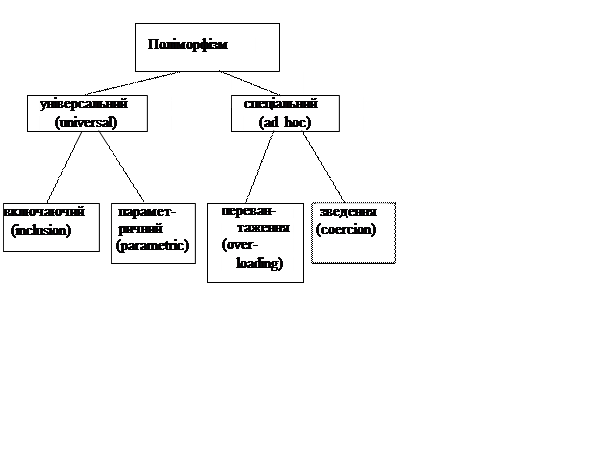
Параметричний поліморфізм зв'язаний з підтримкою родових типів (шаблони в C++).

Включаючий поліморфізм пов'язаний зі спадкуванням і уточненням типів. Єдиною базою для опису поліморфізму може бути λ-вирахування.

6.4 Найпростіше вирахування типів з уточненням λ_≤

Для базових типів будемо використовувати позначення ρ, власне кажучи, ρ є метазмінною. Буквою Γ будемо позначати сукупність тверджень про уже відомі типи виразів.

Визначимо тип

τ ::= ρ | τ₁ →τ₂

і формат виразу

                                    e ::= x | λx:τ .e| e₁ e_{2 ,}

де  e₁e₂  означає застосування  e₁  до  e₂.

            Правила утворення типів:

,

,

.

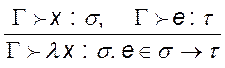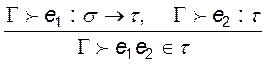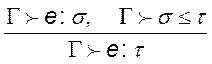            Приклади

            Вираз  S=λx:Integer.x+1 одержує тип  Intege→Integer.

            Вираз twice=λf:Integer.λy:Integer.f(f(y)) одержує тип (Integer → Integer)→( Integer → Integer).

            Аплікація S до 0:  S0 дає значення 1,  яке має тип Integer.

            Аплікація  twice до S: twice(S)= λx.SSx дає вираз типу  Integer → Integer.

6.5 Вирахування типів з перетинаннями λ _^

 

Наступна версія вирахування типів λ_^  дозволяє описувати різновид спеціального поліморфізму, зв'язаний з перевантаженням функцій.

Для скінченного перетинання типів  будемо використовувати позначення .

Тоді множина типових виразів має вигляд

.

            За визначенням вираз e може бути віднесений до типу  тоді і тільки тоді, коли він може бути віднесений до кожного з типів τ_i.

            Правило для типів (typing)

.

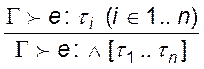            Правила для підтипів (subtyping):

,

,

 .

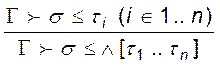            Якщо, наприклад, операція “+” перевантажена для цілих і дійсних чисел, то на рівні реалізації вибирається тип, що більше всього підходить для обчислення виразів.

6.6 Вирахування типів з обмеженою квантифікацією  F_≤

            Термін “з обмеженою квантифікацією” означає “з обмеженням кількості типів”.

            Мова цього типу вирахування поповнюється новим видом формул: . Їх можна трактувати як нескінченне перетинання типових виразів, отриманих з виразу  τ  за  допомогою заміни  змінної  α  на різні підтипи  σ ≤ σ'. На відміну від  λ_≤  і  λ_^  вирахування F_≤ є вирахуванням другого порядку, тому що включає квантифікацію за типами.

            У даному вирахуванні додатково вводяться вирази типової абстракції за типовою змінною α виду  Λα ≤ τ.e і типової конкретизації вигляду e[τ]. Синтаксично ці вирази мало відрізняються від виразів функціональної абстракції й аплікації.

            Вираз  e[τ] означає підставлення типу τ у вираз e замість типової змінної, зв'язаної у зовнішньому абстракторі.