Методології програмування. Основні методології, страница 2

            Визначимо

,

.

Правила для типів:

,

.

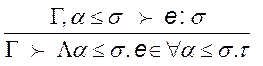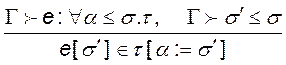Правило для підтипів

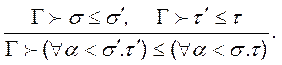
Дане вирахування описує, зокрема,  параметричний поліморфізм.

Приклади опису параметризованих функцій:

1          з типом    ,

2  

      з типом   ,

3  

      з типом .

Застосуємо зазначені параметризовані функції до різних аргументів.

1  id[int](3) = 3.

2  twice1[int](id)(3) = 3.

До S функція twice1 незастосовна.

3  twice2[int] = λ f . int→int . λ x: int . f ( f ( x )),

twice2[int](S) = λ x: int . S ( S ( x )),

twice2[int](S)(3) = 5.

Існують також теорії, де використовуються екзистенціальні типи з виразами вигляду .

Це означає, що реалізація абстрактного типу даних існує і задовольняє обмеження α ≤ τ₁.

Такий підхід дозволяє описувати інкапсуляцію даних.

У даному викладі ми обмежилися синтаксичним рівнем. Однак тип і підтип повинні бути погоджені також і за поводженням.

У загальному випадку поводження функціонального типу може бути описане в термінах передумов і постумов, а поводження об'єктного типу - у термінах передумов і постумов його методів, а також інваріантної умови, що описує властивості, які повинні залишатися незмінними.

6.7Функціональне програмування

Функціональне програмування використовує парадигму, яка повністю відмінна від імперативної. Функціональна програма являє собою деякий вираз, виконання програми означає обчислення цього виразу.

При порівнянні функціонального й імперативного підходів до програмування можна помітити такі властивості функціональних програм.

Функціональні програми не використовують змінних у тому значенні, в якому вони використовуються в імперативному програмуванні. (На рівні машинної мови проміжні змінні існують, однак деталі сховані від програміста). Зокрема у функціональних програмах не використовуються оператори присвоювання. Тому функціональна програма не може мати побічних ефектів.

 Як наслідок з попереднього пункту, у функціональних програмах немає циклів.

Функціональні програми використовують функції більш складним способом. Їх можна передавати в інші функції як аргумент і повертати як результат.

Замість циклів  функціональні програми широко використовують рекурсію.

Єдиним способом поділу програми на частині є введення імені для функції і задання виразу для цього імені.

Вищенаведене стосується чистих функціональних мов, прикладом яких є ранні версії Lisp.

Сучасні функціональні мови, як правило, мають імперативні властивості. Там можуть бути і змінні, і присвоювання, і цикли.

Найбільш відомими серед сучасних функціональних мов є Common Lisp, Scheme, Haskell.

Якщо програма інтенсивно використовує функції, у тому числі логічні, наприклад, в задачах штучного інтелекту, функціональний  підхід має ряд переваг перед імперативним.

Функціональні програми більш безпосередньо відповідають математичним об’єктам, а отже, дозволяють проводити строгі доведення. Установити значення імперативної програми, тобто тієї функції, яку вона реалізує, може виявитися більш складно, ніж функціональної.

Наприклад, розглянемо таку програму на Haskell:

factorial n   =   if n == 0  then 1 else n*factorial(n-1) .

Практично відразу видно, що ця програма відповідає функції

f(n) = n!  для  n≥0  і невизначена для  n<0 .

Для програми на Сі  ця відповідність неочевидна:

int f (int n)

   {

       int x = 1;

       while (n > 0)

       {

      x = x * n;

      n = n – 1;

   }

   return x;

}

Слід зазначити, що функції мови Сі та інших імперативних мов не є строго математичними функціями. Їх значення може залежати не тільки від аргументів. Результатом їх виконання можуть бути різні побічні ефекти (наприклад, зміна значення глобальної змінної). Два виклики однієї і тієї самої функції з одними і тими ж аргументами можуть привести до різних результатів.

Функції у функціональних програмах не мають цих недоліків. Порядок обчислення підвиразів не впливає на результат. Таким чином, при виконанні функціональних програм можна виконувати паралельні обчислення, оскільки окремі компоненти виразів можуть виконуватися одночасно.