Аналіз проблеми інформаційного синтезу систем керування, що навчаються, страница 8

Історично становлення теорії машинного навчання відбувалося із розвитком статистичних методів розпізнавання образів [121-129], що ґрунтуються, головним чином, на байесівському вирішальному правилі  [121-124]. Суть цього правила полягає у порівнянні обчислених в процесі навчання СК апостеріорних імовірностей  , де   - подія, що відображає дійсну належність реалізації образу класу  ; g_l - гіпотеза про належність реалізації класу , . Саме завдяки статистичному підходу відбувся стрімкий розвиток методів і алгоритмів навчання, головною задачею якого був набір статистичних даних з метою формування апріорних імовірностей. Обчислення апостеріорних імовірностей за апріорними здійснюється за відомою формулою Байеса:

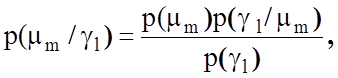                                                                      (1.4.1)

де     –  умовна апріорна ймовірність прийняття гіпотези   за умови існування основної гіпотези  ;

          - повна ймовірність прийняття гіпотези, яка визначається за теоремою про повну ймовірність як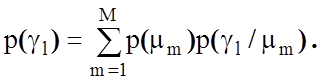 

За байесівським вирішальним правилом гіпотезу  g_l   належить віднести до класу  , якщо апостеріорна ймовірність для цього класу максимальна. Але оскільки оцінка апостеріорних імовірностей здійснюється за вибірковим методом математичної статистики, то це обумовлює ризик помилки особливо у тих випадках, коли центри розсіювання реалізацій образів знаходяться близько один до одного. Тому на практиці приймається  рішення за умови мінімізації функції умовного ризику: 

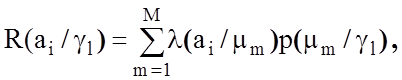                                                             (1.4.2)

де      - функція втрат, яка визначає втрати  а_і , обумовлені прийняттям гіпотези  g_l  за умови, що реалізація образу, яка розпізнається, належить класу  .

         Побудова розбиття    за байесівським правилом здійснюється шляхом обчислення класифікатором роздільних функцій  f(g_l )  і вибору  гіпотези  g_l, для якої роздільна функція є найбільшою. Застосування класифікатора Байеса на практиці є ускладненим, оскільки вигляд функцій щільності ймовірностей, як правило, невідомий. Тому з метою використання класифікатора Байеса розвинулося два підходи: параметричний, при якому функції щільності подаються в аналітичному вигляді, що не завжди можливо, і непараметричний підхід, при якому непотрібне апріорне знання вигляду функції щільності ймовірностей. При непараметричному підході для оцінки основних величин функції щільності користуються або безпосередньо методами математичної статистики [118,], або методами парзенівських вікон [123], радіальними методами (ядра щільності) [63,72], правилом  К  найближчих сусідів [63,123] та іншими [63,72,123]. Для оцінки практичного значення байесівського класифікатора досить послатися на думку визнаного фахівця в галузі технічного зору Ф. Кауфе [202, с.193], який вважає, що застосування байесівського класифікатора навіть з використанням відомих непараметричних методів оцінки функції щільності ймовірностей має «недостатню ступінь успіху для впровадження у виробництво».

Відсутність на практиці повної апріорної інформації про функціональний стан слабо формалізованого процесу, яка повинна включати так само ще і знання про закони розподілу моментів виникнення відхилень і тривалість викидів випадкових величин, є основною причиною низької достовірності розпізнавання за статистичними методами. Найбільш суттєві результати за статистичними методами в області контролю та керування отримано в тих галузях науки і техніки, де є можливість набору репрезентативної статистики при забезпеченні статистичної однорідності та статистичної стійкості, які витікають з центральної граничної теореми теорії ймовірностей [210]. Саме при виконанні умов цієї теореми є можливість застосування добре розробленого апарату теорії статистичних рішень, основаного на параметричних методах математичної статистики. Суть усіх статистичних методів навчання полягає в знаходженні роздільної функції, спосіб побудови якої задає спосіб розбиття простору на класи розпізнавання. Так, наприклад, у працях [63,123] задача навчання трактується як вибір серед можливих вирішальних правил такого, яке мінімізує середній ризик помилкового розпізнавання. З метою збільшення оперативності статистичних алгоритмів класифікації логічним є застосування алгоритмів мінімізації емпіричного середнього ризику, в яких функція емпіричного ризику обчислюється за випадковою та незалежною вибіркою малого обсягу. Але ефективність розв’язання задачі навчання шляхом мінімізації функції емпіричного ризику, як це показано в праці [91], на практиці прямо залежить від умов існування рівномірної збіжності статистичної похибки до заданого значення в класі подій.