Аналіз проблеми інформаційного синтезу систем керування, що навчаються, страница 6

де       n₁, n₂ - обсяги навчальних виборок  класів    відповідно;

 - операторні оцінки умовних щільностей імовірностей для вибірки значень  і-ї ознаки класів    відповідно;

N- кількість ознак розпізнавання.

          Вирішальне правило з урахуванням (1.3.3) має вигляд:

{}Î,  якщо 

{}Î,  якщо 

де       с - вибраний поріг прийняття рішень.

          На жаль, у праці [119] не вдалося встановити аналітичну залежність порогу  с  від точнісних характеристик розпізнавання, а тільки встановлено на нього обмеження:   , де

 =

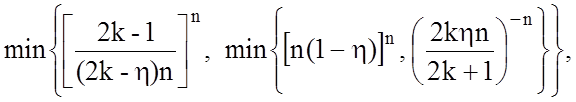
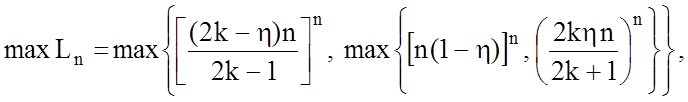
де      k - напіврозмах апроксимації функції розподілу навчальної вибірки:         

k= [1, max{n₁ , n₂}]/2;

          h - ваговий коефіцієнт операторної апроксимації,  0 £h£1.

Таким чином, авторам праць [119,120] вдалося встановити наближений зв’язок між обсягом навчальної вибірки, потужністю словника ознак розпізнавання і точнісними характеристиками розпізнавання. Але отримані результати мають декілька вагомих недоліків, які зменшують їх практичне значення. По-перше, спрощення, пов’язане з вибором однакових операторних параметрів апроксимації  k, h і  h,  де  h- інтервал групування спостережень навчальної вибірки, значно впливає на достовірність розпізнавання на екзамені, оскільки щільність імовірностей оцінок розподілу відношення правдоподібності залежить від значень цих параметрів і потребує у загальному випадку їх адаптації. Виправданням такого спрощення може бути тільки умова наявності однакових дисперсій для всіх ознак розпізнавання в апріорно класифікованих навчальних вибірках, що на практиці, як правило, не має місця і потребує для її забезпечення спеціально організованих заходів. По-друге, якщо головною задачею теорії є побудова алгоритму розпізнавання, який забезпечує збіжність операторної оцінки    до апріорної щільності, то питання отримання задовільної точності оцінювання при скінчених обсягах навчальних вибірок залишилось відкритим, оскільки відсутня однозначна залежність між точнісними характеристиками і операторними параметрами. До речі, мова тут може йти тільки про прийняття компромісного рішення при відомих обмеженнях на параметри апроксимації функції щільності. По-третьє, одним із шляхів покращення збіжності операторної оцінки    до апріорної щільності є вимога  h ® 0, яка без врахування обмеження для параметра  hзліва, може при операторній обробці екзаменаційної (контрольної) вибірки скінченого обсягу призвести до появи порожніх або нерепрезентативних інтервалів групувань даних. Оскільки об’єднаня таких інтервалів виключається запропонованим алгоритмом розпізнавання, то це призведе навпаки до зменшення достовірності розпізнавання і навіть до появи псевдо багатомодальності функції щільності для екзаменаційної вибірки, що виходить за обмеження методу. Один із шляхів подолання цього недоліку полягає в збільшенні обсягу екзаменаційної вибірки, але це суперечить поставленій авторами задачі мінімізації сумарного обсягу навчальних і екзаменаційних вибірок, що забезпечує потрібний гарантований рівень достовірності розпізнавання. І, нарешті, основне обмеження, яке пов’язано з методологією статистичної теорії прийняття рішень і значно звужує практичне значення цього методу синтезу, полягає у виключенні з розгляду гіпотези нечіткої компактності реалізацій образу, яка допускає перетин класів розпізнавання, що є характерним для практичних задач контролю та керування.

У праці [61] розроблено алгоритми оптимізації обсягу та структури екзаменаційної вибірки у задачах контролю та керування складними системами за критеріями максимуму достовірності, мінімуму середніх витрат і за мінімаксними критеріями. Незважаючи на модельність та незавершеність розробки статистичних методів аналізу та синтезу складних систем, застосування теоретико-статистичного підходу до проектування здатних навчатися інтелектуальних систем у науково-методологічному плані є прогресивним, оскільки він орієнтований на розробку методів корекції вхідного математичного опису за умови отримання прийнятної гарантованої достовірності розпізнавання на екзамені. При цьому необхідно підкреслити, що пріоритетність такої постановки і реалізації задачі належить українській школі академіка Івахненка О.Г, яким запропоновано вирішувати проблему моделювання складних систем у рамках методу групового врахування аргументів шляхом пошуку моделі оптимальної складності за допомогою відбору множини моделей-претендентів за критеріями самоорганізації [196-–198].