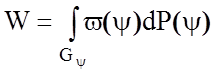Аналіз проблеми інформаційного синтезу систем керування, що навчаються, страница 5

                                                 ,                                        (1.3.1)

де      - множина можливих станів системи;

          w(y) - функція, яка визначає економічні втрати залежно від можливих станів системи;

P(y) - функція розподілу ймовірностей функціональних станів системи.

           Для конкретної СК, яка контролює  n  параметрів і складається з  m  функціональних блоків середні питомі (в одиницю часу) втрати на основі (1.3.1) подаються у вигляді:

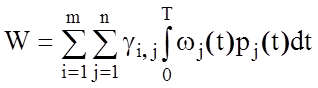                                               ,                                 (1.3.2)

де     w_j (t) - середні питомі втрати від дефекту  j-го параметра;

          p_j(t) - щільність дефекту  j-го параметра;

  g_i,j- знакова функція: g_i,j=1  при відмові  і-го блока, яка викликає порушення контролю  j-го параметра і  g _i,j=0  в протилежному випадку.

         Тоді для оцінки ефективності СК пропонується така нормована величина:

,

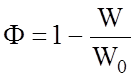де      W - середні втрати, які мають місце при функціонуванні системи і які обчислюються за формулою (1.3.2);

           W₀ - середні втрати у випадку, коли процес контролю або керування здійснюється без використання СК, ефективність якої оцінюється.

           Запропонований у праці [191] метод статистичного синтезу систем контролю та керування має притаманний всім параметричним методам недолік, пов’язаний з необхідністю використання досить “багатої” статистики, яка повинна задовольняти основну статистичну гіпотезу, що на практиці не завжди виконується.

Вперше задачу інформаційного синтезу комп’ютерізованої СК було розглянуто у 1971 році в монографії І.В. Кузьміна [193], в якій пропонувалося оцінювати ефективність системи за узагальненим функціонально-статистичним критерієм. Цей критерій враховує як інформаційну спроможність, яка визначає найважливішу складову загальної ефективності системи - функціональну ефективність, так і зведені витрати на забезпечення прийнятних показників інших складових ефективності. Часткові критерії інформаційної спроможності комп’ютерізованої СК розглянуто у праціі [194]. Так само у працях вітчизняних авторів – В.І Скуріхіна і О.А. Павлова [195], О. Г. Івахненка [196-198], В.І. Костюка В.І. [78,79], В.І. Васильєва [63,89], Ю.П. Зайченка [90], Л.С. Ямпольського [199], І.Б. Сіроджи [96,97], А.С. Куліка [102,103], А.М. Сільвестрова [200],      Е.Г. Петрова [60], Є.П. Путятіна [77] та інших і закордонних авторів, наприклад, [115, 201,202] закладено основи для переходу від методології визначення оператора оброблення даних до сучасної методології аналізу даних, яка знайшла своє втілення в об’єктно-орієнтованому проектуванні складних систем різної природи [203].

         Cуттєві результати в рамках статистичного синтезу отримано у працях [119,120], де розроблено теоретичні основи оптимізації просторово-часових характеристик системи розпізнавання шляхом встановлення кількісних співвідношень між тривалістю процесів навчання. прийняття рішень і розмірністю простору ознак розпізнавання. При цьому мінімізація сумарної кількості реалізацій образу і ознак розпізнавання здійснюється з метою забезпечення достатнього гарантійного рівня достовірності розпізнавання при заданій допустимій міжкласовій відстані. Зупинимось  на розробленому в праці  [119]  непараметричному вирішальному правилі, яке ґрунтується на використанні операторних оцінок як одномірних, так і багатовимірних функцій щільності ймовірностей, отриманих за апріорно класифікованими навчальними вибірками 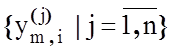   довільних обсягів із генеральних сукупностей значень ознак розпізнавання з апріорно невідомими функціями розподілу класів розпізнавання  . З метою встановлення аналітичного зв’язку між точнісними характеристиками розпізнавання і операторними параметрами апроксимації емпіричних функцій щільності в праці [119] основну увагу приділено знаходженню розподілу оцінок відношення правдоподібності, яке має вигляд:

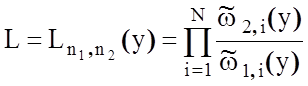                                           ,                                       (1.3.3)