Дослідження алгоритмів побудови складних сигналів Лежандра, Якобі, систем сигналів Уолша та оцінка їх властивостей: Методичні вказівки для проведення лабораторного заняття

Методичні вказівки для проведення лабораторного заняття

з дисципліни: “ЗАБЕЗПЕЧЕННЯ БЕЗПЕКИ ІНФОРМАЦІЇ В ВИСОКОШВИДКІСНИХ СИСТЕМАХ”

Тема: Дослідження алгоритмів побудови складних сигналів Лежандра, Якобі, систем сигналів Уолша та оцінка їх властивостей

Навчальна група: ІБ-04-1, ІБ-04-2, ІБ-04-3

Час: 4 години

Місце: каф. БІТ

Мета заняття: Вивчити структурні характеристики сигналів Лежандра, Якобі, систем сигналів Уолша шляхом моделювання на ЕОМ

Методичні вказівки до організації самостійної роботи.

При підготовці до виконання лабораторної роботи необхідно:

-  вивчити визначення сигналів Лежандра, Якобі, систем сигналів Уолша;

-  вивчити математичний опис сигналів Лежандра, Якобі, систем сигналів Уолша;

-  вивчити основні алгоритми побудови сигналів Лежандра, Якобі, систем сигналів Уолша;

-  підготувати бланк звіту до лабораторної роботи;

-  підготувати відповіді на контрольні питання.

Програма роботи:

1.Дослідити структурні характеристики ансамблів сигналів Лежандра, Якобі, систем сигналів Уолша.

2. Дослідити спектри сигналів Лежандра, Якобі, систем сигналів Уолша.

3. Дослідити автокореляційні функції сигналів Лежандра, Якобі, систем сигналів Уолша.

Теоретичні відомості.

Периодические ФАК ряда кодовых последовательностей обладают интересными свойствами, что проиллюстрируем на примере ненормированной ПФАК, которую определим в виде:

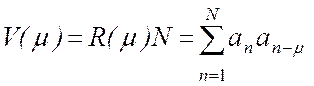.                                      (2.1)

Если обозначить максимальное значение ПФАК (2.1) через , то известны возможные оценки максимального значения:

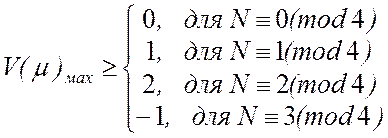.                                (2.2)

В (2.2) сравнения осуществляются по модулю 4(mod4). Кодовые последовательности, у которых ПФАК имеет точное значение  часто называются минимаксными. К минимаксным последовательностям относятся и M-последовательности. В табл. 2.1 приведены известные минимаксные последовательности.

Таблица 2.1

Минимаксные последовательности

Вид последовательности	Период	Примечания
М-последовательности		k – целое           N – простое  число l – целое число   t – целое число    t, t+2 – простые числа
Последовательности Лежандра
Последовательности Холла
Последовательности Якоби

Следует отметить, что если данному периоду N соответствуют различные по виду последовательности, то эти последовательно­сти могут совпадать. Последовательности Якоби в общем случае характери­зуются периодом , где значение l может быть равно 2; 4; 6, но только при l = 2 эти последовательности минимаксные (). Последовательности Якоби с периодом  называются также дважды простыми последовательностями.

Как видно из табл. 2.1, различным N могут соответствовать различные последовательности. В табл. 2.2 указаны виды последовательностей для N, изменяющегося от 3 до 200. Через L обозначены последовательности Лежандра, через J – последовательности Якоби, М соответствует M-последовательности.

Таблица 2.2.  

Виды последовательностей

N	Вид	N	Вид	N	Вид	N	Вид
3	М	35	J	79	L	143	J
7	М	43	L	83	L	151	L
11	L	47	L	103	L	163	L
15	М	59	L	107	L	167	L
19	L	63	М	127	M, L	179	L
23	L	67	L	131	L	191	L
31	M, L	71	L	139	L	199	L

Последовательности Лежандра.

Если 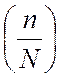 есть символ Лежандра (символ n по отношению к N), то символы последова­тельности Лежандра определяются как

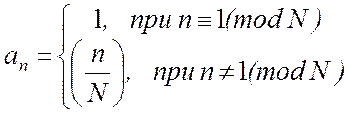.                            (2.3)

Отметим, что в теории чисел символы Лежандра вводятся при рассмотрении уравнений второй степени:

                          ,                                       (2.4)

причем  наибольший общий делитель (n,N)=1. Решить уравне­ние (2.4) означает найти такое х, при котором (2.4) превра­щается в тождество. Сравнение (2.4) имеет решения не при любых значениях n. Значения n, при которых уравнение (2.4) имеет решения, называются квадратичными вычетами, а значе­ния n, при которых (2.4) не имеет решений, называются квад­ратичными невычетами. Символ Лежандра определяется как

.

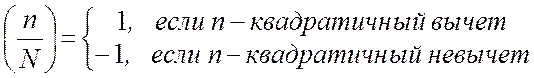Он определен для всех n, не делящихся без остатка на N, при­чем N – простое число, большее двух. Если символ Лежандра найден, то становится известным, имеет ли решение уравнение (2.4) при данном n. Из (2.4) следует, что если число n пред­ставляет собой квадрат какого-то числа по модулю N, то он яв­ляется квадратичным вычетом. Например, для уравнения х² = 17 (mod 19) имеем решение 6²=36=17(mod19), т. е. число 17 – квадратичный вычет. Основные свойства символов Лежанд­ра сводятся к следующим выражениям: