Дослідження ансамблевих та кореляційних характеристик складних ДЧ сигналів: Методичні вказівки для проведення лабораторного заняття

Методичні вказівки для проведення лабораторного заняття

з дисципліни: “ЗАБЕЗПЕЧЕННЯ БЕЗПЕКИ ІНФОРМАЦІЇ В ВИСОКОШВИДКІСНИХ СИСТЕМАХ”

Тема: Дослідження ансамблевих та кореляційних характеристик складних ДЧ сигналів

Навчальна група: ІБ-04-1, ІБ-04-2, ІБ-04-3

Час: 4 години

Місце: каф. БІТ

Мета заняття: Вивчити ансамблеві та кореляційні характеристики складних ДЧ сигналів шляхом моделювання на ЕОМ

Методичні вказівки до організації самостійної роботи.

При підготовці до виконання лабораторної роботи необхідно:

-  вивчити визначення складних ДЧ сигналів;

-  вивчити математичний опис складних ДЧ сигналів;

-  вивчити основні алгоритми побудови складних ДЧ сигналів;

-  підготувати бланк звіту до лабораторної роботи;

-  підготувати відповіді на контрольні питання.

Програма роботи:

1. Отримати систему складних ДЧ сигналів згідно різних правил їх побудови.

2. Дослідити ансамблеві та кореляційні характеристики складних ДЧ сигналів.

Теоретичні відомості.

Наибольшее распространение на практике получили дискретные частотные (ДЧ) сигналы, обладающие только одним час­тотным элементом во временной полосе. Пример такого сигнала приведен на рис. 3.1. Подобные ДЧ сигналы называются сигналами первого порядка.

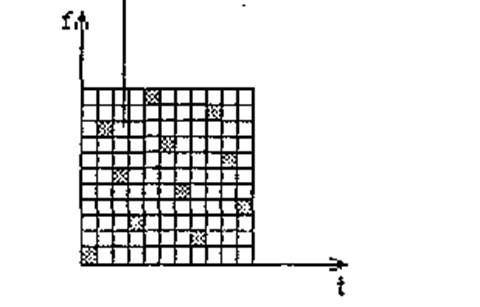
Рис. 3.1.

Положим, что ДЧ сигнал состоит из М элементов, а все элементы имеют одинаковую форму Ф(t). Пусть номера элементов v изменяются от 0 до М-1,  - комплексная амплитуда v-го элемента, а положение v-го элемента по частоте определяется сдвигом, равным , где  - символ частотной кодовой по­следовательности (ЧКП) , причем  при изменении  меняется в таких же пределах, но в определенном по­рядке.

С учетом сделанных предположений комплексная огибающая ДЧ сиг­нала

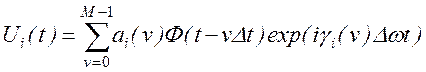                                                                                                 (3.1)

причем здесь и в дальнейшем используется условие , где  - ширина спектра элемента, - его длительность. Смещение соседних элементов по частоте равно , а по времени - . Как видно из (8.1), изменение аргумента у элемента Ф(t) проис­ходит линейно в соответствии с изменением v, a смещение по частоте - в соответствии с изменением . Например, для ДЧ, показанного штриховкой на частотно-временной плоскости (рис. 3.1.), ЧКП .

Известна частотно-временная дуальность ДЧ сигналов. Ис­пользование ее позволяет расширять применение тех или иных по­лученных результатов. Чтобы воспользоваться этим, преобразуем комплексную огибающую ДЧ сигнала, используя временную ко­довую последовательность (ВКП) , к следующему виду:

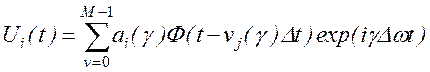                                                                                                 (3.2)

В формуле (3.2) линейно меняется смещение по частоте в со­ответствии с изменением , а изменение аргумента у элемента Ф(t) происходит в соответствии с изменением ВКП , символы которой изменяются в тех же пределах от 0 до М-1, но в определенном порядке. Например, для ДЧ сигнала, изображенного на рис. 8.1, ВКП .

Формулы (3.1) и (3.2) определяют частотно-временную ду­альность ДЧ сигналов: в (3.1) отсчет происходит по времени (по номерам дискретов v), а в (3.2) - по частоте (по сдвигу частоты, пропорциональному )

Алгоритмы построения оптимальных и квазиоптимальных систем ДЧ сигналов были получены на основе теории чисел. В табл. 8.1 приведены алгоритмы построения последовательностей  удовлетворяющих сравнению , , , . В табл. 3.1 приведены правила образования последовательностей ; ограничения, налагаемые на определенные коэффициенты; объем системы и оценка ФВК.

В первой строке табл. 8.1 число  — первообразный корень по модулю простого числа M+1. Все остальные правила основаны на степенных сравнениях по модулю простого числа М. В четвертой строке числа r и М—1 взаимно-простые, т. е. (r, М—1) = 1.

Таблица 3.1.

Алгоритмы построения оптимальных и квазиоптимальных

систем ДЧ сигналов

Правила образования последовательностей	Коэффициенты	Объем системы	Максимум ФВК
		M	1/M
		M—1	1/M
		(M— l)M	2/M
		M—l	1/M
	одновременно		r/M
	; остальные		r/M
	нечетное; ;		r/M

Первая строка табл. 3.1 дает алгоритм построения оптимальной системы с максимальным объемом L, равным числу элементов в сигнале М, а вторая и четвертая строки дают алгоритмы, при которых L=M—1. Остальные строки табл. 3.1 дают алгоритмы построения систем, близких к оптимальным, но большего объема.

Как видно из табл. 3.1, объем оптимальных систем ДЧ сигналов (с одним совпадением) удовлетворяет следующему соотношению

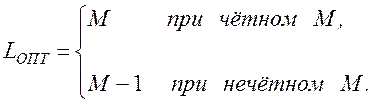                            (3.3)