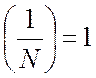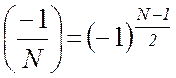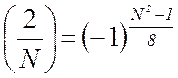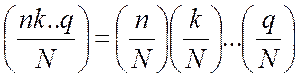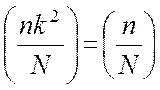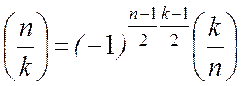Дослідження алгоритмів побудови складних сигналів Лежандра, Якобі, систем сигналів Уолша та оцінка їх властивостей: Методичні вказівки для проведення лабораторного заняття, страница 2

;  ; ; ;

; , если n, k – простые нечетные числа

(n₁/N)=(n/N), если n₁=n(modN)

Отметим, что при nº0(mod N) символ Лежандра не определен.

На рис. 2.1 изображен сигнал Лежандра, построенный согласно последовательности Лежандра для N=19:

1  1  -1  -1  1  1  1  1  -1  1  -1  1  -1  -1  -1  -1  1  1  -1.

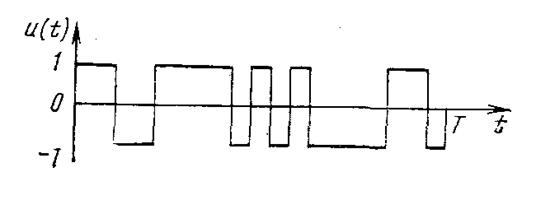
Рис. 2.1. Сигнал Лежандра

Последовательности Лежандра, как и M-последовательности, являются линейными рекуррентными и описываются линейным рекуррентным уравнением вида n = b+(n–1), где b – целое чис­ло. Значение каждого символа последовательности а_n получается путем преобразования n в символ Лежандра 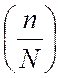, если он опре­делен. Последовательности Лежандра, как и M-последовательности, являются минимаксными.

Последовательность Якоби.

Если символ Якоби

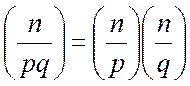                                               (2.5)

где  наибольший общий делитель (n, р, k)=1, a  p, q – простые числа, то последовательность Якоби для p>q определяется как

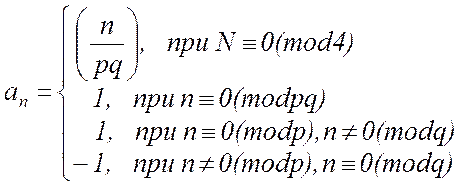(2.6)

Раньше было оговорено, что под последовательностями Якоби будут подразумеваться такие, у которых р = q + 2, период равен N, a n изменяется от 0 до N-1. Так как символ Якоби определяется произведением символов Лежандра, то вычисление его производится согласно правилам определения символов Лежандра.

Например, при р = 7, q = 5 период, N=35, а символы последовательности Якоби за период чередуются следующим образом:

1 1 -1 1 1 -1 -1 1 -1 1 -1 1 1 1 1 -1 1 1 -1 -1 -1 1 -1 -1 -1-1 -1 1 1 1 -1 -1 -1 1 -1.

Легко убедиться, что найденная последовательность Якоби является минимаксной. Соответствующий сигнал изображен на рис. 2.2.

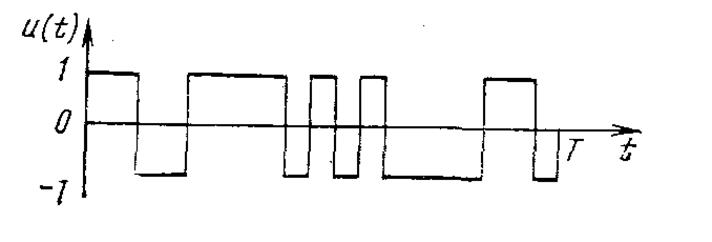
Рис. 2.2. Сигнал Якоби

Последовательности Лежандра и Якоби, а также родственные им исследованы подробно, но они менее распространены по сравнению с M-последовательностями.

Системи Уолша.

Известны системы дискретных ортогональных ФМ сигналов, ортогональность которых определяется выбором формы сигналов. Наиболее распространены ортогональные ФМ сигналы, построенные на базе по­следовательностей (функций) Уолша. Кодовые последо­вательности Уолша можно получить с помощью матрицы Адамара.

Матрицей Адамара называется ортогональная квадратная матрица порядка N, элементами которой являются символы а_n = ±1. Ортогональной называ­ется матрица, строки которой взаимно ортогональны, т. е. каждая строка отображает ортогональную последо­вательность.

Матрицы Адамара определяются следующим сим­волическим равенством:

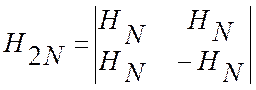                                    (2.7)

где H_N – матрица Адамара порядка N (число строк равно числу столбцов N), а Н_2N – матрица Адамара порядка 2N. Полагая H₁ =1, из (2.7) получаем следующие матрицы порядка 2, 4, 8:

;        ;

.

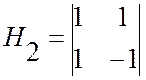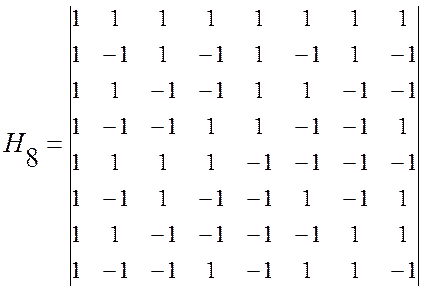Используя (2.7), можно найти матрицы Адамара для любого N=2^m, где m – целое число. Матрицы Адамара известны не толь­ко порядка N = 2^m, но и других значений N. В основном известны матрицы Адамара порядка кратного 4. Матрицы Адамара удовлетворяют уравнению

H_NH^T_N = NI,                                           (2.8)

где Н^T_N  – транспонированная матрица Адамара; I – единичная матрица.

В (2.8) используется обычное произведение матриц. Матрица порядка 2N может быть получена путем применения прямого (или внешнего) произведения матриц. Если Н_N и Н_М – матрицы Адамара порядков N и М, то прямое произведение

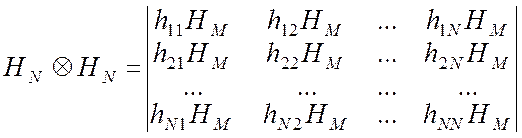,                  (2.9)

где h_jk– элементы матрицы H_N. В (2.9) каждый элемент умно­жается на все элементы матрицы Н_М по правилу умножения мат­рицы на скаляр. Порядок матрицы  равен произведению NM. Из (2.9) следует, что матрица

.                                     (2.10)

Формула (2.10) соответствует символическому равенству (2.7).

В качестве кодовых последовательностей системы Уолша мож­но брать строки или столбцы матрицы Адамара. Число кодовых последовательностей равно порядку матрицы N. Следовательно, объем системы Уолша равен N. Обозначать системы Уолша будем следующим образом: например, У-8, где цифра равна объему.

Обозначим j-ю кодовую последовательность Уолша как {W_j}, а ее n-й символ через W_j(n). Уравнение (2.8) определяет ортого­нальность кодовых последовательностей Уолша, т. е. выполняет­ся равенство

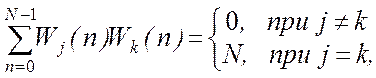                                         (2.11)

Для символов последовательностей Уолша используется следующее мультипликативно-двоичное представление:

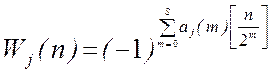,                                  (2.12)

где S = log₂N-1,                                 

[х] – целая часть х, a_j(m) – двоичное представление номера последовательности j.

В формуле (2.12) , . Рас­смотрим пример. Пусть N = 8 для матрицы Адамара. В табл. 2.3 приведены формулы для определения показателя степени W_j(n) при j = const и сами последовательности.

В первом столбце табл. 2.3 приведены номера последователь­ностей  в десятичном счислении, а в трех последующих столбцах – в двоичном счислении. Номера двоичных символов m расположе­ны в порядке возрастания разрядов слева направо так же, как и в сумме показателя степени в (2.12). В пятом столбце приведены формулы для нахождения показателя степени, который равен сум­ме слагаемых вида [n/2^m].