з дисципліни: “ЗАБЕЗПЕЧЕННЯ БЕЗПЕКИ ІНФОРМАЦІЇ В ВИСОКОШВИДКІСНИХ СИСТЕМАХ”
Тема: Дослідження алгоритмів побудови складних сигналів ЛРП та оцінка їх властивості
Навчальна група: ІБ-04-1, ІБ-04-2, ІБ-04-3
Час: 4 години
Місце: каф. БІТ
Мета заняття: Вивчити структурні характеристики сигналів ЛРП шляхом моделювання на ЕОМ
При підготовці до виконання лабораторної роботи необхідно:
- вивчити визначення сигналів лінійних рекурентних послідовностей;
- вивчити математичний опис сигналів ЛРП;
- вивчити основні алгоритми побудови сигналів лінійних рекурентних послідовностей;
- підготувати бланк звіту до лабораторної роботи;
- підготувати відповіді на контрольні питання.
Програма роботи:
1.Дослідити структурні характеристики ансамблів сигналів ЛРП
2.Дослідити спектри сигналів ЛРП максимальної довжини.
3.Дослідити автокореляційні функції сигналів ЛРП.
Теоретичні відомості.
Линейные рекуррентные последовательности и их свойства.
Среди фазоманипулированных сигналов особое место занимают сигналы, кодовые последовательности которых являются последовательностями максимальной длины (ЛРПМ) или М-последовательностями. Такие последовательности обладают следующими основными свойствами:
1. М-последовательность является периодической с периодом, состоящим из N импульсов (символов).
2. Боковые пики периодической автокорреляционной функции сигналов, образованных М-последовательностью, равны -1/N.
3. Последовательность в общем случае состоит из нескольких, видов импульсов (например, импульсы могут отличаться начальными фазами, несущими частотами и т. д.). Импульсы различного вида встречаются в периоде примерно одинаковое число раз, т. е. все импульсы распределяются в периоде равновероятно. Вследствие этого последовательности называют часто псевдослучайными.
4. Структурные свойства:
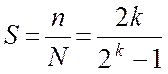
5. Если просуммировать по модулю 2 ЛРПМ со своей циклической сдвижкой, то мы получим ту же самую последовательность, только циклически сдвинутую
6. Формируются М-последовательности с помощью линейных переключательных схем на основе сдвигающих регистров. При этом, если применяется регистр с k разрядами и в М-последовательности используются р различных видов импульсов (отличающихся, например фазами), то
![]() (1)
(1)
Число
разрядов регистра ![]() . Следовательно,
значительное увеличение числа импульсов N в периоде
М-последовательности вызывает незначительное увеличение числа разрядов
регистра, так как зависимость k от N является логарифмической.
. Следовательно,
значительное увеличение числа импульсов N в периоде
М-последовательности вызывает незначительное увеличение числа разрядов
регистра, так как зависимость k от N является логарифмической.
7.
Автокорреляционная функция усеченной М-последовательности, под которой понимается
непериодическая последовательность длиной в период N, имеет величину боковых пиков, близкую к ![]() . Поэтому с ростом N величина боковых пиков
уменьшается.
. Поэтому с ростом N величина боковых пиков
уменьшается.
Фазоманипулированный сигнал с помощью М-последовательностей формируется следующим образом. Каждому символу последовательности ставится в соответствие радиоимпульс со своей начальной фазой. В двоичной системе счисления (р=2) это соответствие можно определить как
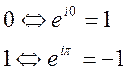 (2)
(2)
где двойная стрелка означает соответствие.
Таблица 1. Умножение символов
|
´ |
1 |
-1 |
|
1 |
1 |
-1 |
|
-1 |
-1 |
1 |
В соответствии с (2) сложение символов 0 и 1 превращается в таблицу умножения символов 1 и -1 (табл. 1).
ПФАК ФМ сигнала равна
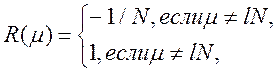 (3)
(3)
где l= 0, 1, ...
На рис. 1,а изображена М-последовательность с N=15, на рис. 1,б - ПФАК, дискретные значения которой построены согласно (3), на рис. 1,в - апериодическая ФАК.
Анализ работы цифрового автомата формирования М-последовательности на основе рекуррентного уравнения показывает, что работа этого автомата полностью определяется характеристическим многочленом
![]() . (4)
. (4)
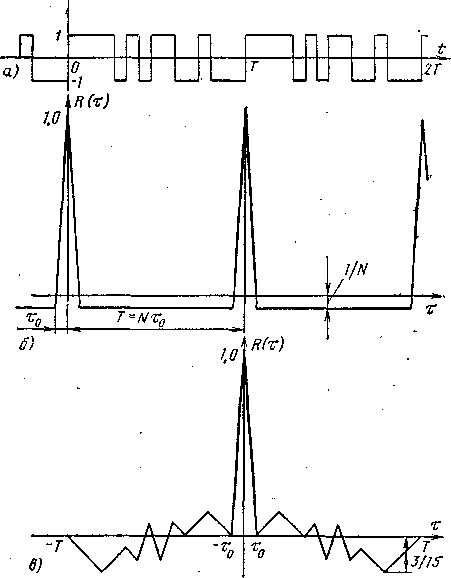
Рис. 1 М-последовательность с ![]() (а),
(а),
периодическая ФАК (б), апериодическая ФАК (в)
Таким образом, для определения
структуры цифрового автомата необходимо знать характеристический многочлен
степени k. Из теории М-последовательностей известно, что характеристический
многочлен f(x) степени k, во-первых,
должен быть неприводимым, т. е. его нельзя представить в виде произведения
многочленов меньших степеней, а во-вторых, он должен быть первообразным
(примитивным) относительно двучлена ![]() , т. е. характеристический
многочлен f(x) должен делить
, т. е. характеристический
многочлен f(x) должен делить ![]() без
остатка. Поэтому характеристический многочлен является первообразным корнем
уравнения
без
остатка. Поэтому характеристический многочлен является первообразным корнем
уравнения ![]() . Если характеристический многочлен является
первообразным, то он является и неприводимым.
. Если характеристический многочлен является
первообразным, то он является и неприводимым.
Таким образом, чтобы при
заданных N, k и р определить структуру регистра для формирования
М-последовательности с периодом ![]() , необходимо в качестве
характеристического многочлена взять первообразный многочлен степени k.
, необходимо в качестве
характеристического многочлена взять первообразный многочлен степени k.
Соответственно период
М-последовательности ![]() . Знание коэффициентов
. Знание коэффициентов ![]() позволяет однозначно построить цифровой автомат
формирования М-последовательностей. Если
позволяет однозначно построить цифровой автомат
формирования М-последовательностей. Если ![]() , то
выход n-го триггера подключен к сумматору по mod 2, если
, то
выход n-го триггера подключен к сумматору по mod 2, если ![]() , то выход n-го триггера к сумматору по mod
2 не подключен.
, то выход n-го триггера к сумматору по mod
2 не подключен.
Для примера на рис. 2 изображена
схема цифрового автомата формирования М-последовательности с ![]() и
и ![]() . В
качестве характеристического многочлена взят многочлен с коэффициентами
10000001001. В соответствии с коэффициентами многочлена на сумматор по mod 2 поступают символы с выходов 7-го и 10-го триггеров.
. В
качестве характеристического многочлена взят многочлен с коэффициентами
10000001001. В соответствии с коэффициентами многочлена на сумматор по mod 2 поступают символы с выходов 7-го и 10-го триггеров.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.