Изучение спектральных закономерностей атома водорода (лабораторная работа), страница 5

п = 1,  ® 1 – состояние,

п = 2,  ® 2и  2р – состояния,

п = 3, ® 3, 3р, 3 – состояния и т.д.

Схема энергетических уровней атома водорода представлена на рисунке 1.2. На схеме отражено частичное вырождение уровней. Видно, что энергия электрона зависит лишь от главного квантового числа.

          По оси ординат на диаграмме отложены значения энергии электрона в электрон – вольтах (эВ).

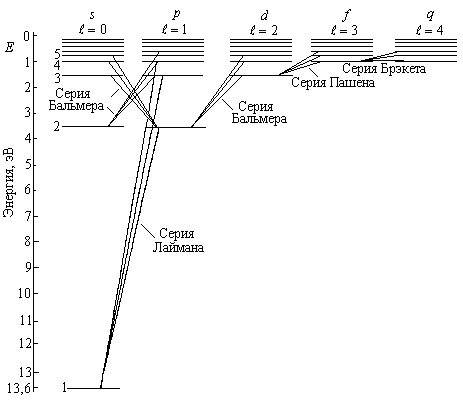
Рисунок 1.2 – Схема энергетических уровней атома водорода

Состояние 1является основным состоянием атома водорода. В этом состоянии атом обладает минимальной энергией. Ее величину можно определить из формулы (1.6) при п = 1:

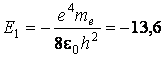 эВ.

          Таким образом, энергия, необходимая для ионизации атома водорода, равна 13,6 эВ.

          Энергию электрона в состояниях с п = 2, 3, 4 и т.д. можно определить также из формулы (1.5), подставив в нее соответствующее значение квантового числа п. Из диаграммы энергетических уровней видно, что с ростом главного квантового числа п уровни сближаются.

          Чтобы перевести атом из основного состояния в возбужденное (т.е. в состояние с большей энергией), ему необходимо сообщить энергию. Это может быть осуществлено за счет теплового соударения атомов или за счет столкновения атома с достаточно быстрым электроном (ускоренным электрическим полем в газовом разряде) или за счет поглощения атомом фотона.

          Фотон при поглощении его атомом передает ему всю свою энергию (фотон неделим), поэтому атом может поглощать только те фотоны, энергия которых в точности равна разности энергий двух его уровней. Поскольку поглощающий атом обычно находится в основном состоянии 1, спектр поглощения водородного атома должен состоять из линий, соответствующих переходам

1®пр  (п = 2, 3, 4 …)

Эти переходы отвечают серии Лаймана. Следовательно, в обычных условиях в спектре поглощения водорода наблюдается единственная серия Лаймана.

          При переходе из состояний с большей энергией в состояние с меньшей энергией атом излучает квант энергии . Длина волны (частота) излучения определяется формулами (1.2), (1.8) или (1.4), (1.7). В квантовой механике доказывается, что для орбитального квантового числа существует правило отбора, согласно которому возможны лишь такие переходы, при которых  изменяется на единицу:

                                                                 .                                                (1.14)

Это связано с тем, что фотон обладает спином, равным , и правило отбора является следствием закона сохранения момента количества движения.

          На рисунке 1.2 показаны переходы, разрешенные правилом (1.14). Пользуясь условными обозначениями состояний электрона, переходы, приводящие к серии Лаймана можно записать в виде:

пр ®1 (п = 2, 3 …).

Это означает, что в формулах (1.2), (1.4), (1.7), (1.8) , .