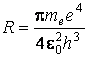Изучение спектральных закономерностей атома водорода (лабораторная работа), страница 4

                                                           (в с^-1),                                         (1.9)

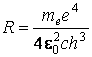                                                           (в м^-1).                                     (1.10)

Значения, предсказанные квантовой механикой, хорошо совпадают с экспериментально найденными.

          Таким образом, постоянная Ридберга представляет величину, пропорциональную энергии атома в основном () состоянии.

          Параметр  называется орбитальным квантовым числом, которое определяет величину (модуль) момента количества движения электрона в атоме по формуле:

                                                              .                                       (1.11)

При заданном главном квантовом числе п орбитальное квантовое число может принимать одно из следующих значений: = 0, 1, 2, …п – 1, т.е. всего п – значений.

          Параметр  называется магнитным квантовым числом и определяет проекцию момента количества движения электрона на некоторое направление  в пространстве по формуле:

                                                               .                                             (1.12)

При данном квантовом числе  квантовое число  может принимать  различных значений, а именно:

.

          Таким образом, атом водорода, находящийся в стационарном состоянии, характеризуемом определенной энергией, может находиться в состояниях, отличающихся модулем М, либо его проекцией

          Состояния с одинаковым значением энергии, но различными значениями модуля момента количества движения или его проекции на некоторое направление  называются вырожденными, а число различных квантовых состояний с одним и тем же значением энергии называется кратностью вырождения соответствующего уровня. Кратность вырождения  уровней атома водорода определяется по формуле:

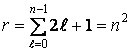                                                              .                                    (1.13)

          В атомной физике используются условные обозначения состояний электрона с различными значениями момента количества движения М. Состояние с  обозначается как – состояние,

  обозначается как – состояние,

  обозначается как – состояние,

  обозначается как – состояние и т.д.

  (по алфавиту)

          При обозначении состояния значение главного квантового числа указывается перед обозначением квантового числа . Поскольку  принимает значения от 0 до п – 1, то возможны следующие состояния: