Изучение спектральных закономерностей атома водорода (лабораторная работа), страница 2

          Частоты всех спектральных линий атома водорода можно представить одной формулой, которая была получена экспериментально и называется обобщенной формулой Бальмера:

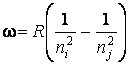                                                       ,                                             (1.1)

где  – циклическая (круговая) частота;

       – постоянная Ридберга. Она равна  с^-1;

       – целые числа, которые для различных серий и различных линий спектра принимают следующие значения:

–   – для серии Лаймана;

–   – для серии Бальмера;

–   – для серии Пашена и т.д.

Таким образом, частоты спектральных линий в серии Бальмера опишутся формулой:

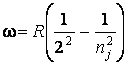                                                            ,                                        (1.2)

где  ….

          В спектроскопе принято характеризовать спектральные линии не частотой, а обратной длине волны величиной:

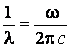                                                                   .                                              (1.3)

Формула Бальмера в этом случае имеет вид:

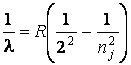                                                                .                                    (1.4)

Постоянная Ридберга  в формуле (1.4) имеет значение  и измеряется в м^-1.

          В таблице 1.1 приведены значения длин волн  серии Бальмера, рассчитанные по формуле (1.4).

          При возрастании  длина волны  стремится к предельному значению , которое называется границей серии. Для серии Бальмера () граница серии обозначается символом .

Таблица 1.1