Численные методы интегрирования: Методические указания к выполнению лабораторной работы № 5, страница 6

                                                                        

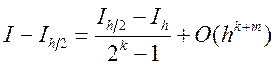
Уточнение Ричардсона, заданное формулой

                                                                  

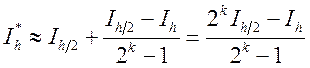
определяется с погрешностью

Тогда неравенством, определяющим область сходимости, будет:

                                                                                     

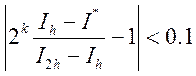
Неравенство может не выполняться по следующим причинам:

1. h велико, при этом влияет неучитываемый член O(h^k+m).
2. h слишком мало, тогда могут сказаться погрешности округлений в вычислениях на ЭВМ, т.е. приближенное значение уже достаточно близко подошло к точному и погрешность метода вычислений равна нулю.
3. с=0 или близко к нулю.

Ответим теперь на следующий вопрос: «Сколько верных цифр нужно взять у результата при вычислении на ЭВМ, совпадающих с верными цифрами точного значения, если точное значение не известно?». Для этого нужно вычислить на ЭВМ приближенно интеграл на трех сетках, соответствующих  длине шага h/2, h, 2h, и принять за точное значение приближенное, посчитанное на сетке с длиной шага h/2. Если неравенство не выполняется, то, как сказано выше, мы находимся не в зоне сходимости, и погрешность Рунге не может нам ничего дать. В этом случае нужно изменить шаг интегрирования h. Если же неравенство выполняется, то вычисляем погрешность Рунге по формуле. Далее определяем те верные знаки, которые при сложении и вычитании с приближенным значением, посчитанным на сетке с шагом h, погрешности Рунге не меняются, и берем от приближенного значения эти знаки.    

Порядок выполнения задания по лабораторной работе

1. Запрограммировать указанный метод, используя его усложненную квадратурную формулу
2. Провести исследование на порядок точности указанного метода. Данные занести в таблицу следующего вида:

Название метода
Аналитическая оценка порядка точности
Отрезок интегрирования

Полином	Аналитическое значение	Число отрезков	Численное значение	Погрешность	Отношение погрешностей	Уточненное решение по Ричардсону	Погрешность уточненного решения
		N

Полиномы использовать степеней . Для каждой степени рассмотреть результат на N=1 и N=2

3. Провести исследование на порядок аппроксимации метода
1. Выбрать сильно осциллирующую (колеблющуюся) функцию (4-5 колебаний на отрезке интегрирования)
2. Аналитически взять интеграл от нее  ()
3. Заполнить следующую таблицу

Число отрезков	Шаг	Значение	Погрешность	Отношение погрешностей	Погрешность по Рунге	Уточненное решение  по Ричардсону	Погрешность уточненного решения	Порядок аппроксимации

            Последовательно увеличивать число шагов интегрирования в 2 раза до тех пор, пока порядок аппроксимации не станет отличаться от теоретического на 15%.

4. Провести исследование на сгущение сетки:
1. Выяснить, в каких промежутках сгущение сетки дает наилучшие результаты: в местах осцилляции или в местах постоянства
2. Выяснить, в каких промежутках: в точках экстремума или в местах быстрого роста требуется увеличение числа отрезков интегрирования
5. Провести исследование, аналогичное п.3, для реализации методов с использованием REAL*8

Замечание: При задании констант двойной точности необходимо задавать их в виде PI=3,14159265358979D00, а также все переменные накопления и результатов объявлять, как REAL*8