Численные методы интегрирования: Методические указания к выполнению лабораторной работы № 5, страница 3

Формулу Симпсона называют также формулой парабол.

Положим , Где F – функция, определяемая . Поскольку , , , то согласно формуле Тейлора с остаточным членом в интегральной форме имеем:

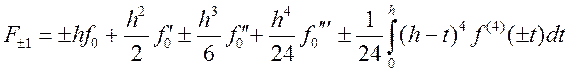
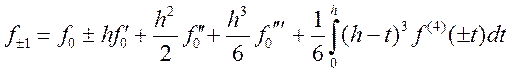
Отсюда получается:

                       

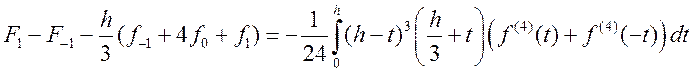
(остальные члены взаимно уничтожаются)

Поскольку , то, применяя теорему и преобразуя полученное значение, получаем:

                                      

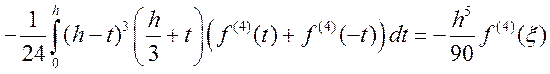
Принимая во внимание, что 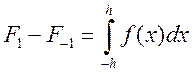, из и приходим к канонической формуле Симпсона с остаточным членом:

                                                                          

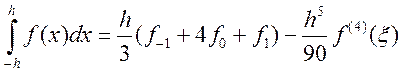
Из формулы очевидно, что порядок точности метода равен 3.

Усложненная квадратурная формула Симпсона

В отличие от метод рассмотренных ранее, положим 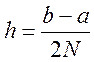 и как обычно , . Перепишем каноническую формулу Симпсона применительно к отрезку  длины  2h.

           

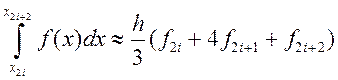
Суммируя левую и правую части этого соотношения по i от 0 до N-1, получаем усложненную квадратурную формулу Симпсона

                                                                      

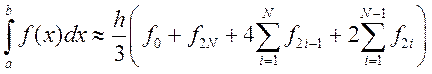
Соответствующая ей формула с остаточным членом:

                                          

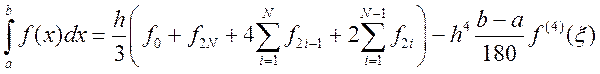
Проведя анализ , выясним, насколько изменится величина остаточного члена при уменьшении h в 2 раза. Подставляя в выражение остаточного члена h/2 вместо h, получаем, что погрешность метода уменьшится в 16 раз, соответственно, порядок аппроксимации метода равен 4.

Многочлены Лежандра

Многочлены, задаваемые выражением

                                                                         

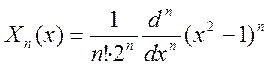
называются многочленами Лежандра.

Они обладают свойством ортогональности на стандартном отрезке

 

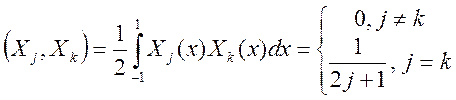
которое проверяется интегрированием по частям.

Лемма.

Многочлен Лежандра степени ортогонален любому алгебраическому многочлену  степени .

Многочлен  является алгебраическим многочленом n-ой степени со старшим коэффициентом, не равным нулю, так как при n-кратном дифференцировании многочлена  степень понижается в точности на n.

Для многочленов Лежандра справедлива рекуррентная формула

по которой с учетом того, что  может быть найден многочлен Лежандра любой степени.

В частности:

                                                                      

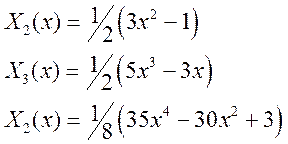
Следующая лемма устанавливает важное свойство многочленов Лежандра, которое нам понадобится в дальнейшем для квадратурных формул Гаусса.

Лемма.

Все корни многочлена Лежандра действительные, простые (однократные) и расположены в интервале

Интерполяционный многочлен Лагранжа.

Пусть известны значения некоторой функции в  различных точках , которые обозначим следующим образом: .

Возникает задача приближенного восстановления функции в произвольной точке . Часто для решения этой задачи строится алгебраический многочлен  степени , который в точках  принимает заданные значения, т.е.

                                                                               

и называется интерполяционным. Точки  называются узлами интерполяции.

Приближенное восстановление функции по формуле  называется интерполяцией функции . Если же  расположен вне минимального отрезка, содержащего все узлы интерполяции , то замену функции  по этой формуле называют экстраполяцией.

Теорема о существовании и единственности интерполяционного многочлена.

Существует  единственный интерполяционный многочлен n-ой степени, удовлетворяющий условиям .

Существование доказывается конструктивно, построением такого многочлена в виде:

                                                                                                 

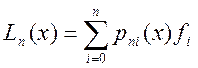
где

                         

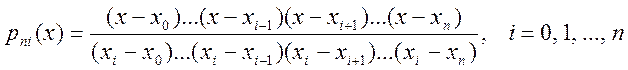
Единственность доказывается от противного.

Интерполяционный многочлен, представленный в виде , называется интерполяционным многочленом Лагранжа, а функции (многочлены) вида – лагранжевыми коэффициентами.