Зная величину остаточного члена можно определить
порядок точности метода. В случае метода прямоугольников его порядок равен 1,
так как ![]() в любой точке
в любой точке ![]() при
степени многочлена не больше 1 равна нулю и формула прямоугольников точна. Для
полиномов более высоких порядков остаточный член нулю не равен.
при
степени многочлена не больше 1 равна нулю и формула прямоугольников точна. Для
полиномов более высоких порядков остаточный член нулю не равен.
Формула называется канонической формулой прямоугольников.
На практике, если требуется вычислить приближенно интеграл , то обычно область интегрирования [a;b] разбивают на N равных частичных отрезков, на каждом из которых применяют
одну из канонических квадратурных формул и суммируют полученные результаты.
Построенная таким образом квадратурная формула называется усложненной.
При применении метода прямоугольников длину частичного отрезка удобно принять
за 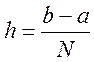 .
.
Пусть функция f дважды непрерывно дифференцируема на [a;b], т.е. ![]() . Обозначим частичные
отрезки, как
. Обозначим частичные
отрезки, как ![]() , где
, где ![]() ,
, ![]() . В соответствии с полагаем:
. В соответствии с полагаем:
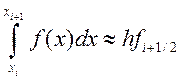
где ![]() - значение функции в
середине частичного отрезка. При этом справедливо равенство, аналогичное , выражающее остаточный член формулы.
- значение функции в
середине частичного отрезка. При этом справедливо равенство, аналогичное , выражающее остаточный член формулы.
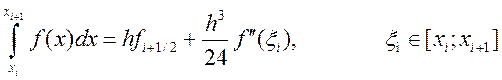
Суммирование по все отрезкам приближенного равенства приводит к усложненной квадратурной формуле прямоугольников.
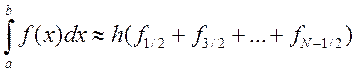
А суммирование равенств , с учетом того, что 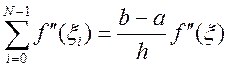 , дает усложненную формулу прямоугольников
с остаточным членом:
, дает усложненную формулу прямоугольников
с остаточным членом:
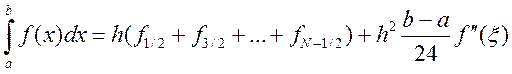
Отсюда видно, что при уменьшении шага в два раза остаточный член уменьшится в 4. Значит, порядок аппроксимации метода равен 2.
Допустим, что ![]() . Положим приближенно
. Положим приближенно
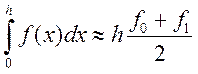
 где
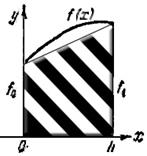
где ![]() , то есть интеграл
заменяется площадью заштрихованной трапеции, изображенной на рисунке 2.
, то есть интеграл
заменяется площадью заштрихованной трапеции, изображенной на рисунке 2.
Выразим ![]() и
и ![]() , где F – функция
определяемая .
, где F – функция
определяемая .
По формуле Тейлора с остаточным членом в интегральной форме:
|
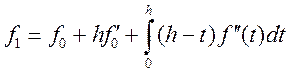
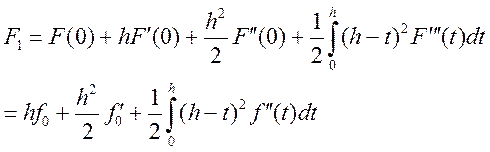
Из выражений и , с учетом того, что ![]() – первообразная
– первообразная ![]() , получаем:
, получаем:
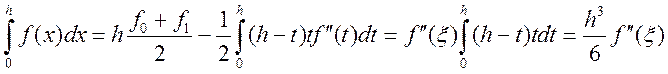
выражение остаточного члена формулы трапеций. Таким образом, мы пришли к канонической формуле трапеций с остаточным членом.
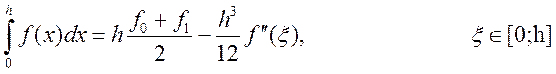
Зная величину остаточного члена, определим порядок точности метода. Он равен 1, т.к. для любого полинома степени более 1, остаточный член нулю не равен.
Аналогично методу прямоугольников разобьем промежуток интегрирования на N равных частей. И просуммируем все значения, полученные на каждом из отрезков в соответствии с и .
Усложненная квадратурная формула трапеций
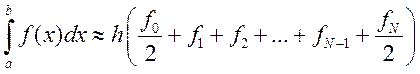
и с остаточным членом:
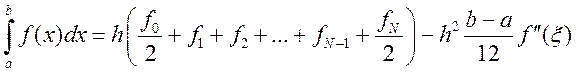
где ![]() .
.
Анализируя , можно сделать вывод, что порядок аппроксимации метода трапеций совпадает с порядком аппроксимации метода прямоугольников и равен 2.
Предположим, что ![]() . Интеграл
. Интеграл 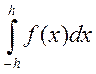
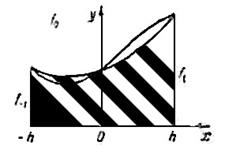 приближенно заменяем площадью заштрихованной
криволинейной трапеции (рис. 3), ограниченной сверху параболой , проходящей
через точки
приближенно заменяем площадью заштрихованной
криволинейной трапеции (рис. 3), ограниченной сверху параболой , проходящей
через точки ![]() ,
, ![]() ,
, ![]() , где
, где ![]() .
Указанная парабола задается уравнением
.
Указанная парабола задается уравнением 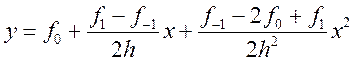 .
Отсюда легко находим:
.
Отсюда легко находим:
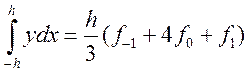 .
.
Таким образом, каноническая формула Симпсона имеет вид:
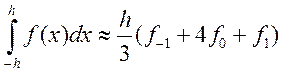
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.